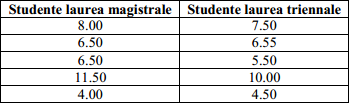
Si è interessati a stimare la differenza $\mu_X-\mu_Y$ tra le spese medie sostenute dagli studenti di laurea magistrale e di laurea triennale per il pasto di mezzogiorno. A tal fine si seleziona un campione di 5 coppie di studenti, uguali per sesso, ceto, provenienza geografica; si rileva la spesa (in Euro) sostenuta per il pasto di mezzogiorno nella giornata di rilevazione:
- Si fornisca la definizione di "stimatore per intervallo" di un generico parametro $\theta$. (risoluzione)
- Si determini un intervallo di confidenza al 99% per $\mu_X-\mu_Y$ (risoluzione)
Punto a)
Uno stimatore per intervallo per un parametro di una popolazione è una funzione delle variabili campionarie che determina gli estremi di un intervallo di valori che verosimilmente contiene il parametro da stimare. La stima corrispondente viene chiamata stima per intervallo.
Punto b)
Dalla tabella si ricavano i seguenti dati campionari: $$\begin{array}{l} \overline{x}=\frac{8.00+6.50+6.50+11.50+4.00}{5}=7.3\\ \overline{y}=\frac{7.50+6.55+5.50+10.00+4.50}{5}=6.81\\ s_x^2=\frac{8.00^2+6.50^2+6.50^2+11.50^2+4.00^2-5\cdot 7.3^2}{5-1}=7.575\\ s_y^2=\frac{7.50^2+6.55^2+5.50^2+10.00^2+4.50^2-5\cdot 6.81^2}{5-1}=4.443\\ s^2=\frac{(5-1)7.575+(5-1)4.443}{5+5-2}=6.009\\ \nu=5+5-2=8\\ 1-\alpha=0,99\ \Rightarrow\ \frac{\alpha}{2}=0.005\ \Rightarrow\ t_{8,0.005}=3.355\end{array}$$ (vai qui per vedere come calcolare il valore critico $t_{\nu,\frac{\alpha}{2}}$)
dove $\overline{x}$ e $s_x^2$ sono rispettivamente il valor medio e la varianza campionarie delle spese per il pranzo sostenute dagli studenti di laurea magistrale, mentre $\overline{y}$ e $s_y^2$ sono rispettivamente il valor medio e la varianza campionarie delle spese sostenute dagli studenti di laurea triennale e $\nu$ sono i gradi di libertà.
Allora, utilizzando la formula per il calcolo dell'intervallo di confidenza per la differenza tra due medie con varianze delle popolazioni incognite, si ha: $$7.3-6.81\pm 3.355\sqrt{6.009\left(\frac{1}{5}+\frac{1}{5}\right)}=0.49\pm 5.2014=[-4.7114;5.6914]$$

10.000 eserciziformazione completa
Eserciziari di Matematica Generale, Analisi I e II, Statistica, Fisica e Algebra Lineare

Altri esercizi di statistica

Densità congiunta della somma di 2 distribuzioni uniformi in (0,1)
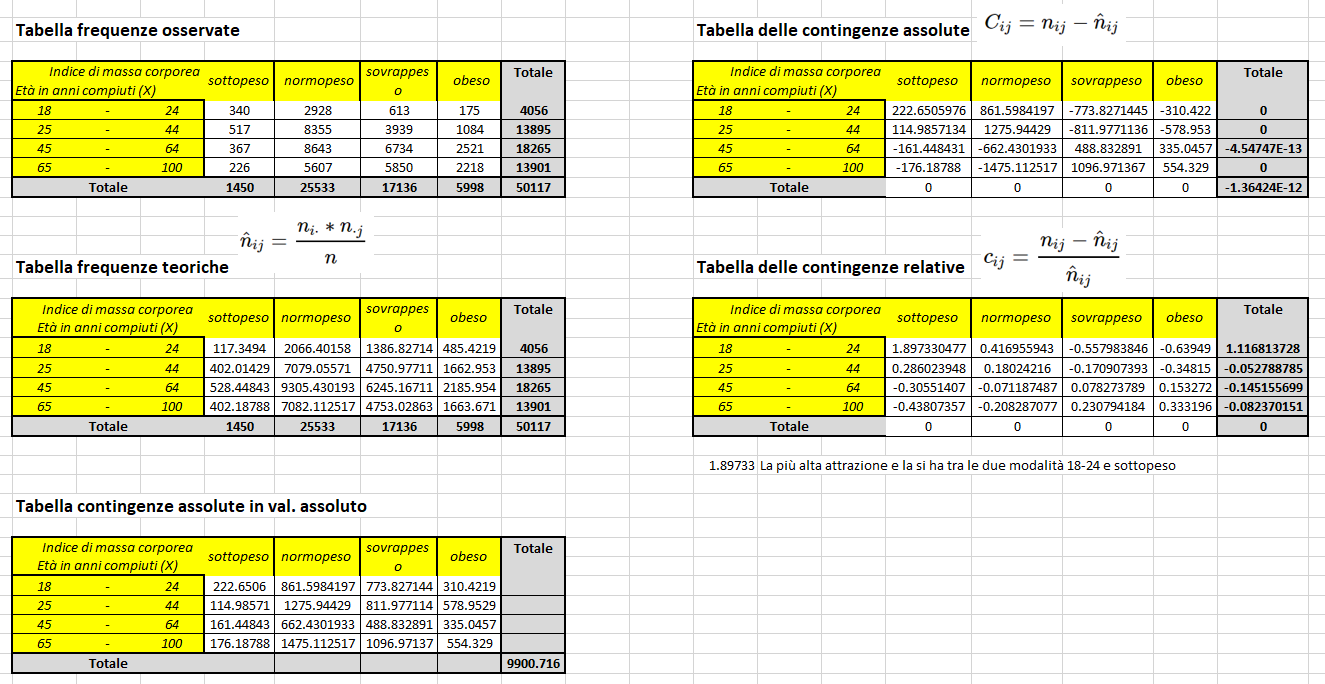
Esercizio sull'indice di connessione di Mortara
Distribuzione uniforme nel cerchio di raggio unitario

Esercizi sul test di ipotesi per la differenza tra due medie
Esercizi sulla disuguaglianza di Cebicev risolti

Esercizi sulla funzione di densità e funzione di distribuzione risolti

Esercizi sull'intervallo di confidenza per la media

Esercizi sull'intervallo di confidenza per la differenza tra due medie