La covarianza tra due caratteri statistici $X$ e $Y$ numerici quantitativi indica la tendenza che questi hanno ad associarsi. Dati $n$ coppie di osservazioni $(x_i,y_i)$ dei caratteri $X$ e $Y$ la covarianza si calcola facendo la sommatoria dei prodotti degli scarti di $X$ e di $Y$ fratto $n$. In formule: $$\bbox[#ffffff,5px,border:2px solid #ff6600]{COV(X,Y)=\cfrac{\sum\limits_{i=1}^n(x_i-\overline{x})\cdot (y_i-\overline{y})}{n}}\quad\LARGE\star$$ dove $\overline{x}$ e $\overline{y}$ sono rispettivamente la media di $X$ e la media di $Y$, ossia:$$\begin{array}{l}\overline{x}=\cfrac{x_1+x_2+\dots + x_n}{n}\\ \overline{y}=\cfrac{y_1+y_2+\dots + y_n}{n}\end{array}$$
Con riferimento alla formula $\LARGE\star$ possiamo analogamente definire la covarianza come la media aritmetica dei prodotti degli scarti delle due variabili $X$ e $Y$, infatti, espandendo la sommatoria si ottiene: $$COV(X,Y)=\cfrac{(x_1-\overline{x})\cdot (y_1-\overline{y})+\dots +(x_n-\overline{x})\cdot (y_n-\overline{y})}{n}$$
Interpretazione statistica della covarianza
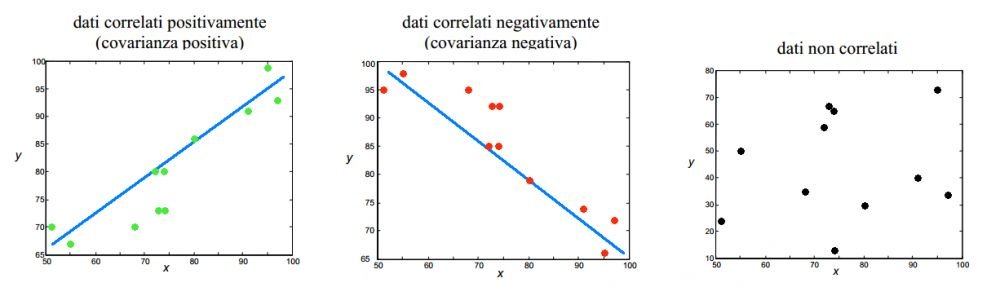
Correlazione positiva o diretta
Abbiamo detto che la covarianza misura la tendenza dell'associazione tra due variabile casuali. Se tale tendenza fa si che "valori grandi" (rispetto il valore atteso) di X si accostino a valori grandi di Y, oppure "valori piccoli" (rispetto il valore atteso) di X con valori piccoli di Y, la covarianza è maggiore di 0. In questo caso si dice che X e Y sono correlate positivamente. In parole più semplici diremo che X e Y sono correlati positivamente o esiste una correlazione diretta se all'aumentare (o al diminuire) di $X$ aumenta (o diminuisce) anche Y
Correlazione negativa o inversa
Se invece all'aumentare (o al diminuire) di X Y, al contrario, diminuisce (o aumenta) la covarianza è minore di 0 si parla di correlazione inversa. In questo caso le variabili aleatorie X e Y in questione si dicono correlate negativamente.
Incorrelazione
Infine, due variabili aleatorie $X$ e $Y$ si dicono incorrelate se la loro covarianza è nulla:
$$COV(X,Y)=0$$ In questo caso si dice che l'associazione tra X e Y è nulla.
Quanto appena detto può essere sintetizzando dai seguenti grafici a dispersione o scatterplot. In particolare, se i dati sono correlati positivamente, i punti $(x_i,y_i)$ si dispongono vicino a una retta crescente; se invece sono correlati negativamente si dispongono lungo una retta decrescente mentre invece se non sono correlati sono sparpagliati nel piano senza seguire nessun andamento lineare.
Misura della forza della correlazione
Tuttavia, la covarianza, essendo un indice di associazione assoluto, non ci permette di capire quanto i dati sono correlati. Per tale motivo si fa ricorso a indici relativi come il coefficiente di correlazione di Pearson il quale ci indica appunto la forza dell'associazione che intercorre tra le due variabili. Te ne ho parlato più in dettaglio in questa lezione.
Formula veloce per il calcolo della covarianza
Per semplificare e velocizzare i calcoli si può far uso della seguente formula operativa per calcolare la covarianza: $$COV(X,Y)=\cfrac{\sum\limits_{i=1}^nx_iy_i-n\cdot\overline{x}\cdot\overline{y}}{n}$$
dove $\overline{x}$ e $\overline{y}$ sono rispettivamente i valori medi di X e di Y.
Covarianza per una tabella di frequenza congiunta
Ci sono casi in cui viene fornita una tabella a doppia entrata contenente le frequenze assolute congiunte di X e Y come del tipo che vedi qui sotto
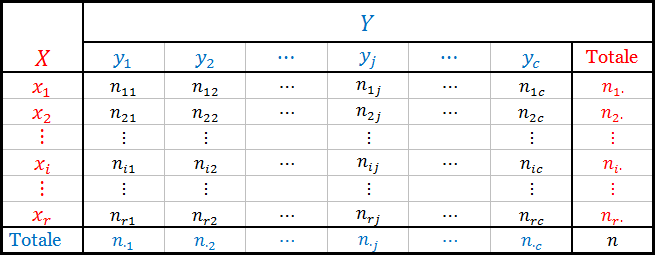
In questo caso devo adattare la formula della covarianza precedentemente scritta introducendo le frequenze assolute congiunte, ossia: $$COV(X,Y)=\cfrac{\sum\limits_{j=1}^c\sum\limits_{i=1}^rx_i\cdot y_j\cdot n_{ij}-n\cdot\overline{x}\cdot\overline{y}}{n}$$
Covarianza tra due variabili aleatorie
Un altro modo di definire la covarianza è tramite il momento centrale misto, ovvero: $$\bbox[#ffffff,5px,border:2px solid #ff6600]{COV(X,Y)=E[(X-E(X))(Y-E(Y))]}$$ dove con la lettera E si indica il valore atteso già precedentemente visto qui (clicca!)
Si dimostra che la covarianza può essere calcolata più semplicemente mediante la seguente formula:
$$COV(X,Y)=E(XY)-E(X)E(Y)$$
Infatti, applicando le proprietà del valor medio e osservando che $E(X)$ ed $E(Y)$ sono delle costanti, si ha:
$\begin{array}{l} COV(X,Y)&=E[(X-E(X))(Y-E(Y))]=E[XY-X\cdot E(Y)-Y\cdot E(X)+E(X)\cdot E(Y)]=\\ &=E(XY)-E[X\cdot E(Y)]-E[Y\cdot E(X)]+E[E(X)\cdot E(Y)]=\\ &=E(XY)-E(X)\cdot E(Y)-E(Y)\cdot E(X)+E(X)\cdot E(Y)=E(XY)-E(X)E(Y)\end{array}$
Proprietà della covarianza
Mediante l'uso della definizione si dimostra che la covarianza gode delle seguenti proprietà:
- La covarianza tra due variabili aleatorie X e Y indipendenti è nulla $$X,Y\ \mbox{indipendenti}\quad\Rightarrow\quad COV(X,Y)=0$$
- La covarianza tra una variabile aleatoria X e se stessa coincide con la varianza di X $$COV(X,X)=VAR(X)$$
- La covarianza tra una variabile aleatoria X e qualsiasi costante a vale 0 (pertanto una costante e un numero aleatorio sono sempre incorrelati) $$COV(X,a)=0$$
- Due costanti a e b sono sempre incorrelate $$COV(a,b)=0$$
Covarianza tra somme di più numeri aleatori
Supponiamo di avere:
$$X=\sum\limits_{i=1}^na_iX_i\quad\quad Y=\sum\limits_{j=1}^mb_jY_j$$
Si ha che la covarianza tra somme è data dalla seguente formula
$$COV(X,Y)=\sum\limits_{i=1}^n\sum\limits_{j=1}^ma_ib_jCOV(X_i,Y_j)$$
Dimostrazione
$\begin{array}{l} COV(X,Y)&=E\left(\sum\limits_{i=1}^na_iX_i\cdot\sum\limits_{j=1}^mb_jY_j\right)-E\left(\sum\limits_{i=1}^na_iX_i\right)E\left(\sum\limits_{j=1}^mb_jY_j\right)=\\ &=E\left(\sum\limits_{i=1}^n\sum\limits_{j=1}^ma_ib_jX_iY_j\right)-\left(\sum\limits_{i=1}^na_iE(X_i)\cdot\sum\limits_{j=1}^mb_jE(Y_j)\right)=\\ &=\sum\limits_{i=1}^n\sum\limits_{j=1}^ma_ib_jE(X_i,Y_j)-\sum\limits_{i=1}^n\sum\limits_{j=1}^ma_ib_jE(X_i)E(Y_j)=\\ &=\sum\limits_{i=1}^n\sum\limits_{j=1}^ma_ib_j\left[E(X_iY_j)-E(X_i)E(Y_j)\right]=\sum\limits_{i=1}^n\sum\limits_{j=1}^ma_ib_jCOV(X_i,Y_j)\end{array}$
Per finire, scriviamo la formula per il calcolo della varianza della somma di due variabili aleatorie dipendenti.
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{VAR(X+Y)=VAR(X)+VAR(Y)+2COV(X,Y)}$$
Osserviamo che, nel caso di variabili aleatorie dipendenti, il termine $COV(X,Y)\neq 0$. È quindi fondamentale introdurlo nella formula precedente a differenza invece del caso di variabili aleatorie indipendenti in cui la covarianza risulta essere nulla.



