Si definisce varianza della variabile aleatoria $X$ il valore atteso del quadrato della differenza tra $X$ e la media $\mu$, ovvero
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{\sigma^2=VAR(X)=E\left[(X-\mu)^2\right]}$$
dove $\mu$ è il valor medio di $X$.
La radice quadrata non negativa della varianza è chiamata scarto quadratico medio o deviazione standard di $X$:
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{\sigma=\sqrt{VAR(X)}=\sqrt{E\left[(X-\mu)^2\right]}}$$
La varianza è un indice di dispersione dei valori della variabile aleatoria X attorno al valor medio $\mu$.
Più tali valori sono concentrati attorno al valore medio, minore sarà la varianza. Viceversa, più lontano si trovano i valori, maggiore sarà la varianza.
Il grafico seguente mostra due esempi di funzione di densità di variabili aleatorie con lo stesso valor medio ma varianza differente.
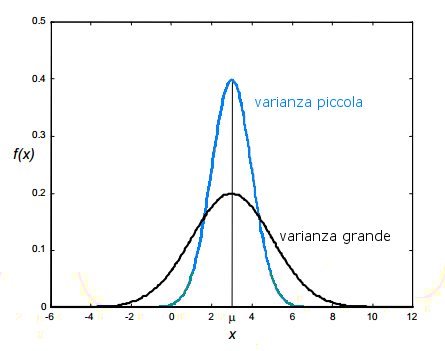
Varianza e scarto quadratico medio nel caso discreto
Sia $X$ una variabile aleatoria discreta, i cui valori possibili sono $x_1,x_2,\dots ,x_n$ assunti rispettivamente con probabilità $f(x_1),f(x_2),\dots ,f(x_n)$.
Chiamiamo varianza della variabile aleatoria X avente valor medio $\mu$ la quantità
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{\sigma^2=\sum\limits_{i=1}^n(x_i-\mu)^2f(x_i)}$$
Si definisce scarto quadratico medio o deviazione standard la quantità
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{\sigma=\sqrt{\sum\limits_{i=1}^n(x_i-\mu)^2f(x_i)}}$$
La varianza può essere calcolata in un modo che talvolta risulta più comodo da usare negli esercizi. Infatti si ha:
$\begin{array}{l} \sigma^2 &=\sum\limits_{i=1}^n(x_i-\mu)^2f(x_i)=\sum\limits_{i=1}^n\left(x_i^2-2x_i\mu+\mu^2\right)f(x_i)=\sum\limits_{i=1}^n x_i^2f(x_i)-2\mu\sum\limits_{i=1}^n x_if(x_i)+\mu^2\sum\limits_{i=1}^n f(x_i)=\\ &=\sum\limits_{i=1}^n x_i^2f(x_i)-2\mu^2+\mu^2=\sum\limits_{i=1}^n x_i^2f(x_i)-\mu^2\end{array}$
Esempio di calcolo della varianza di una variabile aleatoria discreta
Trovare la varianza della variabile aleatoria X definita come il numero di teste ottenute con tre lanci successivi di una moneta.
Svolgimento
Calcoliamo la distribuzione di probabilità.
I casi possibili sono $2^3=8$ ovvero:
- CCC (X=0)
- TCC (X=1)
- CTC (X=1)
- CCT (X=1)
- TTC (X=2)
- CTT (X=2)
- TCT (X=2)
- TTT (X=3)
Per cui, la distribuzione di probabilità sarà:

Possiamo calcolare il valore atteso:
$\mu=E(X)=0\cdot\frac{1}{8}+1\cdot\frac{3}{8}+2\cdot\frac{3}{8}+3\cdot\frac{1}{8}=\frac{3}{8}+\frac{3}{4}+\frac{3}{8}=\frac{3}{2}$
Infine calcoliamo la varianza:
$\sigma^2=VAR(X)=\sum\limits_{i=1}^4\left(x_i-\frac{3}{2}\right)^2=\left(-\frac{3}{2}\right)^2\frac{1}{8}+\left(1-\frac{3}{2}\right)^2\frac{3}{8}+\left(2-\frac{3}{2}\right)^2\frac{3}{8}+\left(3-\frac{3}{2}\right)^2\frac{1}{8}=\frac{3}{4}$
Varianza e scarto quadratico medio nel caso continuo
Sia $X$ una variabile aleatoria continua con densità di probabilità $f(x)$.
Si definisce varianza della variabile aleatoria continua $X$ il seguente integrale:
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{\sigma^2=E\left[(X-\mu)^2\right]=\int\limits_{-\infty}^{+\infty}(x-\mu)^2f(x)\ dx}$$
Si definisce scarto quadratico medio o deviazione standard della variabile aleatoria continua $X$ la radice quadrata della sua varianza:
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{\sigma=\sqrt{\int\limits_{-\infty}^{+\infty}(x-\mu)^2f(x)\ dx}}$$
Anche in questo caso si può usare la forma semplificata per calcolare la varianza:
$$\sigma^2=\int\limits_{-\infty}^{+\infty}x^2f(x)\ dx-\mu^2$$
Esempio di calcolo della varianza di una variabile aleatoria continua
Data la densità di probabilità $$f(x)=\begin{cases} \frac{2(x+1)}{3} & \mbox{se } 0 < x < 1\\ 0 & \mbox{altrimenti}\end{cases}$$ trovare il valor medio e la varianza
Svolgimento
Applicando le formule esposte sopra si ha:
$\begin{array}{l} \mu=\int\limits_0^1x\cdot\frac{2(x+1)}{3}\ dx=\frac{2}{3}\int\limits_0^1(x^2+x)\ dx =\frac{2}{3}\left[\frac{x^3}{3}+\frac{x^2}{2}\right]_0^1=\frac{2}{3}\left(\frac{1}{3}+\frac{1}{2}\right)=\frac{5}{9}\\ \sigma^2=\int\limits_0^1x^2\cdot\frac{2(x+1)}{3}\ dx-\left(\frac{5}{9}\right)^2=\frac{2}{3}\int\limits_0^1(x^3+x^2)\ dx-\frac{25}{81}=\frac{13}{162}\end{array}$
Proprietà della varianza per variabili aleatorie indipendenti
Sia $X$ e $Y$ due variabili aleatorie indipendenti e $a,b\in\mathbb R$. Valgono le seguenti:
- $VAR(aX+b)=a^2VAR(X)$
- $VAR(aX-b)=a^2VAR(X)$
- $VAR(aX+bY)=a^2VAR(X)+b^2VAR(Y)$
- $VAR(aX-bY)=a^2VAR(X)+b^2VAR(Y)$
Analogamente a quanto fatto per il valor medio, la varianza di qualsiasi combinazione lineare di variabili aleatorie indipendenti $X_1,X_2,\dots ,X_n$ si calcola così:
$$VAR(a_1X_1,a_2X_2,\dots ,a_nX_n)=a_1^2VAR(X_1)+a_2^2VAR(X_2)+\dots +a_n^2VAR(X_n)\quad\quad a_1,a_2,\dots ,a_n\in\mathbb R$$
Si noti che, a differenza della varianza, il valore atteso è una funzione lineare.
Infine, si dimostra che il valore atteso del quadrato di un numero aleatorio si può calcolare come segue:
$$E(X^2)=VAR(X)+[E(X)]^2$$
Come si vede, quest'ultima formula mette in relazione la varianza con il valore atteso.
Scopri come calcolare la varianza per eventi dipendenti cliccando qui



