Si dice che una variabile aleatoria continua $X$ ha distribuzione uniforme nell'intervallo $[a,b]$ (con $a,\ b\in\mathbb R$) e si indica con $X\sim U[a,b]$, se la sua densità di probabilità è così fatta:
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{f(x)=\begin{cases} \frac{1}{b-a} & \mbox{se } x\in [a,b]\\ 0 & \mbox{se } x\not\in [a,b]\end{cases}}$$
Qui in basso puoi anche vedere il grafico della funzione di densità di una variabile con distribuzione uniforme:
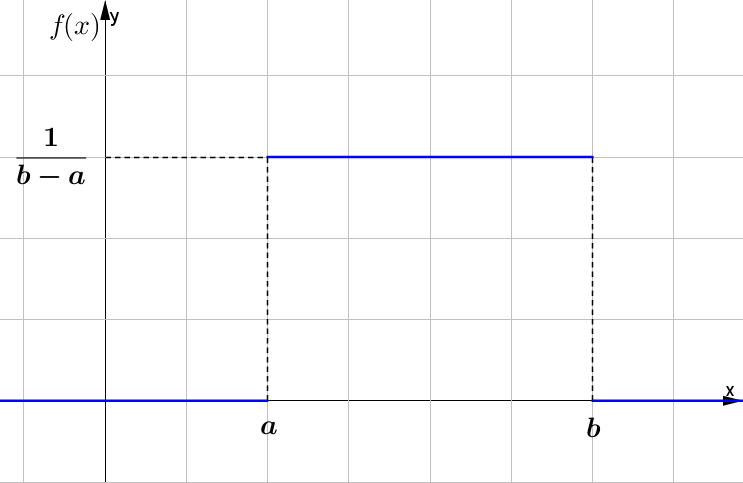
Invece, la funzione di ripartizione della variabile uniforme è:
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{F(x)=P(X\le x)=\begin{cases} 0 & \mbox{se } x\le a\\ \frac{x-a}{b-a} & \mbox{se } a < x < b\\ 1 & \mbox{se } x\ge b\end{cases}}$$
E il seguente è il suo grafico:
Grazie alla funzione di ripartizione possiamo calcolare la probabilità che la variabile aleatoria continua uniforme assuma valori all'interno di un intervallo qualsiasi $[a',b']$ contenuto interamente in $[a,b]$:
$$P(X\in [a',b'])=\frac{b'-a'}{b-a}$$
Esempio 1
Se $X\sim U[0,10]$ la probabilità che $X\in [2,3]$ è:
$$P(X\in [2,3])=\frac{3-2}{10-0}=\frac{1}{10}$$Ovviamente, se l'intervallo $[a',b']$ non fosse contenuto interamente in $[a,b]$, si considererebbe soltanto l'intervallo intersezione dei due.
Esempio 2
Se $X\sim U[4,10]$ la probabilità che $X\in [2,6]$ è:
$$P(X\in [2,6])=P(X\in [4,6])\frac{6-4}{10-4}=\frac{1}{3}$$
Valore atteso e varianza della distribuzione uniforme
Il valore atteso di una variabile aleatoria con distribuzione uniforme nell'intervallo $[a,b]$ è
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{E(X)=\frac{a+b}{2}}$$
Tale risultato si ottiene facilmente applicando la definizione di valore atteso di una variabile aleatoria continua che ricordiamo essere $$E(X)=\int_{-\infty}^{+\infty}xf(x)\ dx$$
Mentre, la varianza di una variabile aleatoria continua con distribuzione uniforme nell'intervallo $[a,b]$ è:
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{VAR(X)=\frac{(b-a)^2}{12}}$$
Quest'ultimo risultato si può ottenere sapendo che $$VAR(X)=E(X^2)-E^2(X)$$




