In questo articolo ti mostro come determinare il dominio di funzioni del tipo:
- razionali intere e fratte;
- irrazionali;
- logaritmiche;
- esponenziali;
- trigonometriche (con seno, coseno e tangente);
- trigonometriche inverse (con arcoseno, arcocoseno e arcotangente).
Vuoi andare direttamente agli esercizi svolti? Clicca qui in basso.
Puoi anche guardare il video qui sotto dove ti mostro come calcolare il dominio di alcune funzioni particolari.
Inizierò col dare delle indicazioni generali per determinare il campo di esistenza in base al tipo di funzione che si presenta. Dopodiché illustrò alcuni esempi pratici sulla determinazione del campo di esistenza.
Per determinare il dominio o campo di esistenza di una funzione $f(x)$ bisogna trovare l'insieme di quei valori della variabile $x$ tali per cui la $f(x)$ abbia significato ed escludere, quindi, quei valori di $x$ per i quali la $f(x)$ risulta essere non definita. In particolare:
- Le frazioni del tipo $\frac{h(x)}{g(x)}$ hanno come dominio l'insieme delle $x$ tali che il denominatore è diverso da zero, ovvero $g(x)\neq 0$ poiché in matematica non sono ammesse le divisioni per zero.
- Le radici del tipo $\sqrt[n]{f(x)}$ con $n$ pari sono definite solo nell'insieme delle $x$ tali che il radicando è maggiore o uguale a zero ovvero il dominio si calcola imponendo $f(x)\ge 0$, poichè non possiamo calcolare le radici di numeri negativi.
- Le funzioni logaritmiche del tipo $\log_b f(x)$ hanno senso solo se l'argomento del logaritmo è strettamente maggiore di zero, ossia, il dominio in questo ultimo caso si calcola imponendo che $f(x)>0$. Infatti per definizione di logaritmo l'argomento non può essere negativo o uguale a zero.
- La funzione trigonometrica tangente del tipo $\tan[f(x)]$ ha come dominio tutti quei valori di $x$ che rendono il suo argomento diverso da pi greco mezzi più eventuale molteplicità, ossia: $$f(x)\neq\frac{\pi}{2}+k\pi$$
- Le funzioni trigonometriche inverse di seno e coseno ossia arcoseno e arcocoseno, sono definite per tutti quei valori di $x$ per i quali i loro argomenti stanno nell'intervallo $[-1,1]$. In sostanza, il dominio delle funzioni del tipo $\arcsin[f(x)]$ e $\arccos[f(x)]$ è $-1\leq f(x)\leq 1$
Nel caso in cui la funzione in esame richiedesse l'imposizione di due o più condizioni, il dominio si calcola facendone il sistema.
Calcolo del dominio di funzioni fratte
Calcoliamo il dominio delle seguenti funzioni
- $f(x)=\cfrac{x^2-x+4}{2x-1}$
- $f(x)=\cfrac{x+1}{x^2+2x-8}$
- $f(x)=\cfrac{x+3x^2}{x^2+1}$
Svolgimento 1: $f(x)=\cfrac{x^2-x+4}{2x-1}$
La funzione si presenta sotto forma di frazione, il cui denominatore può annullarsi. Quindi, per trovare il dominio, dobbiamo imporre che il denominatore deve essere diverso da zero:
$$2x-1\neq 0\quad\Leftrightarrow\quad 2x\neq 1 \quad\Leftrightarrow\quad x\neq\frac{1}{2}$$
Per graficare il dominio della funzione, disegniamo la retta verticale $x=\frac{1}{2}$ con una croce in corrispondenza del punto $\left(\frac{1}{2},0\right)$ per evidenziare che la funzione non interseca tale retta.

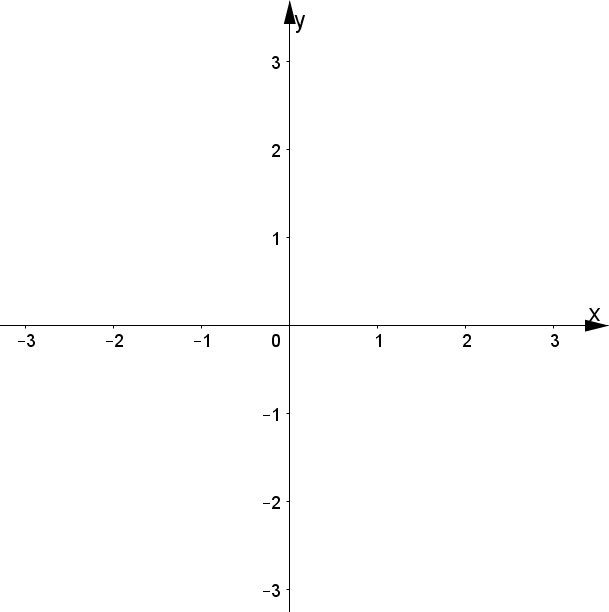
Svolgimento 2: $f(x)=\cfrac{x+1}{x^2+2x-8}$
Analogamente al caso precedente, poniamo il denominatore diverso da 0 e risolviamo la disuguaglianza: $$x^2+2x-8\neq 0\quad\Leftrightarrow\quad x\neq-4\ \wedge\ x\neq 2$$
Stavolta, per graficare il dominio, dobbiamo disegnare le due rette $x=-4$ e $x=2$ in corrispondenza delle quali faremo una crocetta:

Svolgimento 3: $f(x)=\cfrac{x+3x^2}{x^2+1}$
L'ultima funzione è invece definita per ogni valore di $x$ dato che il denominatore $x^2+1$ non si annulla per alcun valore della detta variabile. Per tale motivo, il grafico di questo dominio sarà costituito solo dagli assi cartesiani.
Calcolo del dominio di funzioni irrazionali
Calcoliamo il dominio delle seguenti funzioni
- $f(x)=\sqrt{x^2-4x+3}$
- $f(x)=\sqrt[3]{x^2+5x}$
- $f(x)=\frac{6\sqrt{x+1}+7\sqrt{4-x}}{x^2-7x+6}$
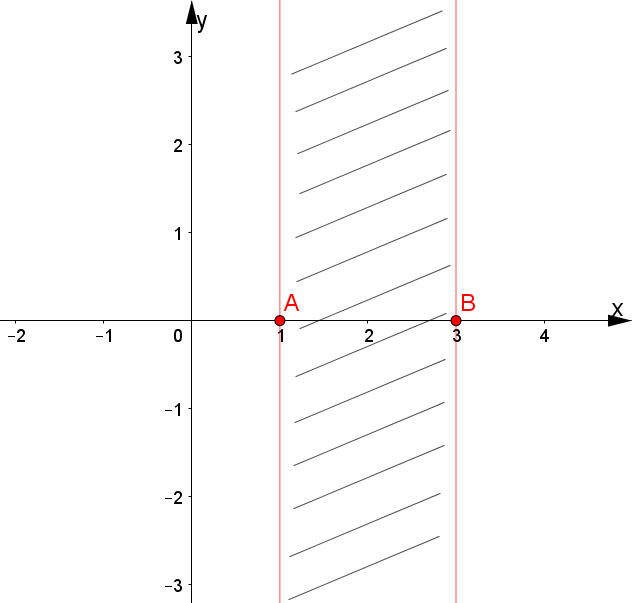
Svolgimento 1: $f(x)=\sqrt{x^2-4x+3}$
Poichè il radicale della prima funzione è di indice pari, la funzione è definita per quei valori di $x$ soddisfacenti la disequazione di secondo grado $$x^2-4x+3\geq 0\ \Rightarrow\ x\leq 1\ \vee\ x\geq 3$$
Il suo grafico consiste in due porzioni di piano distinte poste una alla sinistra della retta $x=1$ e l'altra alla destra della retta $x=3$. Di conseguenza, l'intervallo $(1,3)$ è escluso dal grafico e può essere cancellato: ciò significa che nell'intervallo $(1,3)$ non ci sarà nessun punto della funzione. Invece, i punti $A(1;0)$ e $B(3;0)$ sono appartenenti al grafico, ossia sono punti della funzione.
Svolgimento 2: $f(x)=\sqrt[3]{x^2+5x}$
Il dominio della seconda funzione, invece, è $\forall x\in\mathbb{R}$ dato che l'indice del radicale è dispari. Graficamente, il dominio sarà rappresentato da tutto il piano cartesiano.
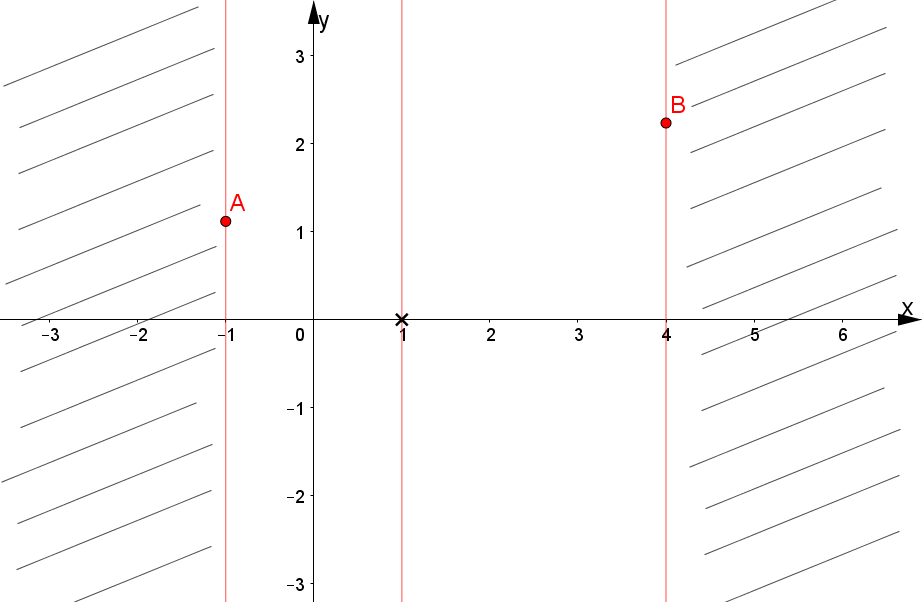
Svolgimento 3: $f(x)=\frac{6\sqrt{x+1}+7\sqrt{4-x}}{x^2-7x+6}$
La funzione è irrazionale fratta ed entrambi i radicali sono di indice pari; essa è pertanto definita per i valori di x soluzioni del sistema: $$\begin{cases} x+1\geq 0\\ 4-x\geq 0\\ x^2-7x+6\neq 0\end{cases}$$ e quindi per i valori di x soddisfacenti le condizioni $$\begin{cases} x\geq -1\\ x\leq 4\\ x\neq 1\ \wedge\ x\neq 6\end{cases}$$
Riportiamo sulla retta reale le soluzioni appena trovate e segniamo in blu la parte a comune:

Il campo di esistenza sarà dunque $-1\leq x\leq 4\ \wedge x\neq 1$. Inoltre, risulta utile calcolare il valore assunto dalla funzione agli estremi del dominio, ossia nei punti $x=-1$ e $x=4$: $$\begin{eqnarray*} f(-1)&=&\frac{6\sqrt{-1+1}+7\sqrt{4-(-1)}}{(-1)^2-7(-1)+6}=\frac{\sqrt{5}}{2}\\ f(4)&=&\frac{6\sqrt{4+1}+7\sqrt{4-4}}{4^2-7\cdot 4+6}=-\sqrt{5}\end{eqnarray*}$$
Deduciamo che i punti $A\left(-1;\frac{\sqrt{5}}{2}\right)$ e $B(4,\sqrt{5})$ sono punti appartenenti al dominio della funzione che rappresentiamo qui sotto:
Calcolo del dominio di funzioni logaritmiche
Calcoliamo il dominio delle seguenti funzioni
- $f(x)=\frac{\log 2x +1}{x}$
- $f(x)=\log(16-x^2)$
Svolgimento 1: $f(x)=\frac{\log 2x +1}{x}$
la funzione presenta un doppio problema: un denominatore e la presenza di un logaritmo. Per risolvere il primo bisogna porre il denominatore diverso da zero, per risolvere il secondo bisogna porre l'argomento del logaritmo maggiore di zero. Entrambe le condizioni vanno messe a sistema:
$$\begin{cases} x\neq 0\\ 2x > 0\end{cases}\quad\Leftrightarrow\quad \begin{cases} x\neq 0\\ x > 0\end{cases}\quad\Leftrightarrow\quad x >0$$
Tale dominio viene rappresentato escludendo dal grafico la parte di semipiano con $x\le0$ (vedi figura qui sotto).

Svolgimento 2: $f(x)=\log(16-x^2)$
La funzione logaritmica è definita per tutti quei valori di $x$ che rendono il suo argomento maggiore di $0$, quindi il dominio si trova svolgendo la disequazione di secondo grado: $$16-x^2>0\ \Rightarrow\ -4 < x < 4$$
Il suo grafico di funzione si compone di un'unica porzione di piano compresa tra le rette $x=-4$ e $x=4$. Inoltre, in corrispondenza di tali rette dobbiamo tracciare una croce per indicare l'esclusione delle ascisse $\pm 4$ dal grafico.

Calcolo del dominio di funzioni esponenziali
Calcoliamo il dominio delle seguenti funzioni
- $f(x)=2^{x+1}$
- $f(x)=3^{\frac{x}{x+1}}$
- $f(x)=(x+4)^x$
Svolgimento 1: $f(x)=2^{x+1}$
La prima è una funzione esponenziale a base numerica positiva e pertanto è definita per ogni valore di $x$.
Svolgimento 2: $f(x)=3^{\frac{x}{x+1}}$
Anche la seconda è una funzione esponenziale a base numerica positiva; essa è definita per ogni valore di $x$, eccetto per lo zero del denominatore dell'esponente, e quindi per ogni $x\neq 1$ (omettiamo il grafico perché la sua rappresentazione consiste semplicemente nel disegnare la retta $x=1$ ed escluderla dal grafico ponendo una croce su di essa).
Svolgimento 3: $f(x)=(x+4)^x$
Affinché sia definita la terza funzione, deve essere $$x+4>0\ \Rightarrow\ x>-4$$
Il suo diagramma giace perciò tutto alla destra della retta $x=4$ (devo quindi cancellare tutta la regione di grafico a sinistra di tale retta).
Calcolo del dominio di funzioni trigonometriche
Calcoliamo il dominio delle seguenti funzioni
- $f(x)=\sin\left(x+\frac{\pi}{2}\right)$
- $f(x)=\frac{1}{\cos x}$
- $f(x)=\tan\left(3x+\frac{\pi}{4}\right)$
Svolgimento 1 e 2: $f(x)=\sin\left(x+\frac{\pi}{2}\right)$, $f(x)=\frac{1}{\cos x}$
Le prime due funzioni sono entrambe trigonometriche e periodiche di periodo $2\pi$. La prima è definita per ogni valore di $x$, mentre la seconda per i valori di $x$ per i quali risulta $\cos x\neq 0$ e pertanto per ogni $x\neq\frac{\pi}{2}+k\pi$. Il suo grafico si compone di infiniti rami separati l'uno dall'altro dalle rette $x=\frac{\pi}{2}+k\pi$.
Svolgimento 3: $f(x)=\tan\left(3x+\frac{\pi}{4}\right)$
Il dominio della terza funzione, essendo la tangente non definita a $\frac{\pi}{2}$, si trova ponendo il suo argomento diverso da pigreco mezzi appunto: $$3x+\frac{\pi}{4}\neq \frac{\pi}{2}+k\pi\ \Rightarrow\ x\neq\frac{\pi}{12}+k\frac{\pi}{3}$$
Calcolo del dominio di funzioni trigonometriche inverse
Calcoliamo il dominio della funzione $$f(x)=\arcsin\frac{x-1}{x}$$
Svolgimento: $f(x)=\arcsin\frac{x-1}{x}$
Tale funzione è definita per quei valori di $x$ tali che l'argomento $\frac{x-1}{x}$ sia compreso tra -1 e 1 ed inoltre deve essere pure $x\neq 0$. Mettendo a sistema le due condizioni suddette $$\begin{cases} -1\leq\frac{x-1}{x}\leq 1\\ x\neq 0\end{cases}\ \Leftarrow\ \begin{cases} \frac{x-1}{x}\leq 1\\ \frac{x-1}{x}\geq -1 x\neq 0\end{cases}$$ e risolvendo otteniamo $x\geq\frac{1}{2}$.



