Abbiamo visto qui come effettuare la divisione tra due polinomi. Quando il polinomio divisore è un binomio del tipo $x-a$, dove $a$ è un numero reale qualunque, per determinare $Q$ ed $R$ possiamo utilizzare un procedimento rapido, detto regola di Ruffini, che permette di calcolare i coefficienti del polinomio $Q$ e il resto $R$.
Esempio
Applicazione della regola di Ruffini
Vogliamo eseguire la divisione: $$(-10x-9+3x^2):(x-4)$$ dove il divisore è del tipo $x-a$.
Innanzitutto scriviamo i polinomi ordinati in senso decrescente: $$(3x^2-10x-9):(x-4)$$
Scriviamo su una riga, nell'ordine, i coefficienti dei termini del dividendo, +3 e -10, e il termine noto -9 inserendoli in una tabella tipo questa di seguito:

A sinistra della prima linea verticale, sulla seconda riga, scriviamo +4, ossia l'opposto del termine noto del divisore $x-4$. Abbassiamo +3, ossia il primo coefficiente del dividendo.
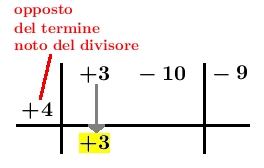
Moltiplichiamo +3 per +4 e scriviamo il risultato nella colonna successiva a +3, ossia sotto -10:
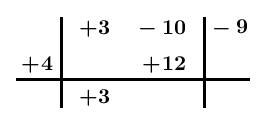
Sommiamo -10 e +12 e scriviamo il risultato (+2) nella stessa colonna, sotto la linea orizzontale:
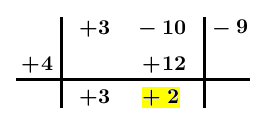
Ripetiamo il procedimento moltiplicando +2 per +4 e scrivendo il risultato nella colonna a destra di +2, sopra la riga orizzontale:
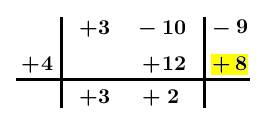
Sommiamo -9 e +8 e scriviamo il risultato nella stessa colonna, sotto la linea orizzontale: -1 è il resto:
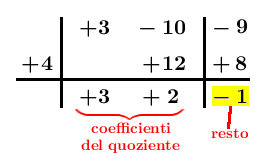
I coefficienti del polinomio quoziente sono 3 e 2. Tenendo conto che il quoziente deve avere grado 1 (uno in meno rispetto al quello del dividendo), possiamo scrivere: $$Q=3x+2;\quad R=-1$$
Per verificare che il risultato sia corretto, controlliamo che sia valida l'uguaglianza $$\begin{array}{l} A=B\cdot Q+R\\ 3x^2-10x-9=(x-4)(3x+2)+(-1)\end{array}$$
Se il divisore è del tipo $x+a$, basta porre: $$x+a=x-(-a)$$
Ad esempio: $$\begin{array}{l} (8x^2+2x-3):(x+2)=\\ =(8x^2+2x-3):[x-(-2)]\end{array}$$
Si può dunque applicare la regola di Ruffini.
Nell'esempio fatto sopra, abbiamo messo in riga i coefficienti del polinomio dividendo $$3x^2-10x-9,\quad\mbox{cioè }3,\ -10,\ -9$$
Se il polinomio dividendo fosse stato incompleto, al posto dei coefficienti mancanti avremmo dovuto mettere gli 0. Per esempio, per il polinomio dividendo $2x^4-x^2-1$, i coefficienti da mettere in riga sono:
Teorema del resto
Data la divisione $$A(x):(x-a)$$ il resto è dato dal valore che assume $A(x)$ quando alla variabile si sostituisce il valore $a$: $$R=A(a)$$
Per capirlo, consideriamo la divisione fatta nell'esempio in alto. Sappiamo che:
$$(-10x-9+3x^2):(x-4)=(3x+2)+(-1)$$
Il teorema del resto dice che, se sostituiamo al posto dell'incognita $x$ del dividendo $-10x-9+3x^2$ il valore $4$ (termine noto del divisore $x-4$ cambiato di segno), otteniamo il resto $R=-1$, infatti:
$$-10(4)-9+3(4)^2=-40-9+48=-1$$
Da questo risultato si deduce il teorema di Ruffini:
Teorema di Ruffini
Un polinomio $A(x)$ è divisibile per un binomio $x-a$ se e soltanto se $A(a)=0$.
Infatti, per definizione, se $A(x)$ è divisibile per $x-a$, il resto $R=0$ e, quindi, per il teorema del resto il polinomio calcolato in $a$ si annulla (ovvero $A(a)=0$).
Esempio
Applicazione del teorema di Ruffini.
Il polinomio $A(x)=2x^3+x^2-5x+2$ è divisibile sia per $x-1$ sia per $x+2$; infatti: $$\begin{array}{l} A(1)&=2+1-5+2=0;\\ A(-2)&=2(-8)+4-5(-2)+2=-16+4+10+2=0\end{array}$$
Vai alla scomposizione dei polinomi mediante regola di Ruffini



