Prima di leggere questo articoli ti consigliamo di consultare la parte introduttiva sui polinomi che trovi in questo link
Somma e differenza tra polinomi
La somma di due polinomi è il polinomio che ha per termini tutti i termini dei polinomi addendi; la differenza è il polinomio ottenuto addizionando al primo l'opposto del secondo. In genere parliamo di somma algebrica.
Esempio
Esempio sulla somma e differenza tra polinomi.
$$\begin{array}{l} &(5x+4y)+(2x-y)-(x+8y)=\\ &=5x+4y+2x-y-x-8y=\\ &=(5+2-1)x+(4-1-8)y=6x-5y\end{array}$$Prodotto tra polinomi
Per ottenere il prodotto di due polinomi si moltiplica ogni termine del primo per ogni termine del secondo. In particolare, il prodotto di un monomio per un polinomio si ottiene moltiplicando il monomio per ogni termine del polinomio:

Esistono alcuni prodotti detti notevoli chiamati tali perchè è possibile calcolarli in modo rapido (vedi qui per approfondimento).
Divisione tra due polinomi
Il procedimento studiato per la divisione tra due polinomi, $A:B$, ci permette di ottenere il polinomio quoziente $Q$ e il polinomio resto $R$, in modo che valga la relazione:
$$A=B\cdot Q+R$$
Precisiamo che la divisione con resto tra due polinomi può essere svolta se e soltanto se il grado del polinomio dividendo è maggiore o uguale al grado del polinomio divisore (ovvero, il grado di $A$ è maggiore o uguale del grado di $B$).
Esempio
Esempio di divisione in colonna tra 2 polinomi
Calcoliamo la seguente divisione
$$(3x^2-x-1):(x-2)$$Dividiamo $3x^2$ per $x$ ($3x^2:x=3x$) e scriviamo il quoziente parziale $Q_1=3x$. Per calcolare la divisione $3x^2:x$ più facilmente, rispondiamo alla seguente domanda: per cosa devo moltiplicare $x$ affinchè risulti $3x^2$? La risposta è $3x$ poichè $x\cdot 3x=3x^2$.

Moltiplichiamo $3x$ per ogni termine di $B$ e scriviamo col segno cambiato i risultati sotto $A$, incolonnati, rispetto al grado, con i termini di $A$:

Sommiamo in colonna i termini, ottenendo un primo resto parziale $R_1=-7x-1$.

Ripetiamo il procedimento partendo da $R_1$. Dividiamo $-7x$ per $x$, ottenendo come secondo quoziente parziale $Q_2=-7$.
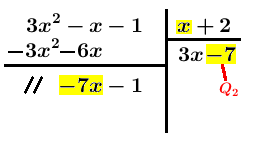
Moltiplichiamo $-7$ per tutti i termini di $B$ e li scriviamo col segno cambiato, in colonna sotto $R_1$.

Eseguiamo l'addizione e otteniamo il resto finale $R=13$. La divisione è conclusa poichè il grado di $R$ (0) è minore del grado di $B=x+2$ (1).
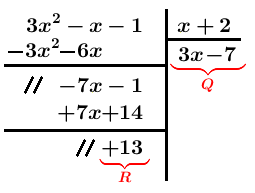
La relazione $A=B\cdot Q+R$ ci permette di verificare l'esattezza del risultato. Dobbiamo infatti calcolare:
$$(x+2)(3x-7)+13$$e controllare che sia uguale a
$$3x^2-x-1$$Lasciamo a voi questa semplice verifica.
Se il divisore di un polinomio è del tipo $x-a$ o $x+a$ possiamo applicare la regola di Ruffini (fai click!).



