L'indice di concentrazione di Gini, al contrario degli indici di dispersione, è un coefficiente che misura il livello di concentrazione di un fenomeno in una distribuzione di dati. Viene spesso utilizzato per verificare se variabili come il reddito o la ricchezza siano più o meno equidistribuiti in una popolazione. Si parla infatti di bassa e alta concentrazione.
Diremo infatti che la ricchezza ha una bassa concentrazione se tende a distribuirsi uniformemente su tutti gli individui mentre diciamo che ha un'alta concentrazione se è nelle mani di poche persone.
Si parla invece di equidistribuzione se il fenomeno o la variabile hanno la più bassa concentrazione possibile: questo accade se ciascun individuo possiede la stessa quantità della media dei dati; mentre, si dice che la concentrazione è massima se un solo individuo ha tutta la quantità e gli altri nulla.
L'indice di Gini è sempre compreso tra 0 (caso di equidistribuzione) e 1 (caso di massima concentrazione) e cresce al crescere del livello di concentrazione.
Formula e calcolo dell'indice di Gini
Denotiamo con $x_1,x_2,\dots ,x_n$ l'ammontare del carattere (ad esempio il reddito) per ciascuna delle $n$ unità statistiche ($i=1,\dots , n$) e supponiamo che siano già ordinati in modo crescente, cioè: $$x_1\le x_2\le \dots \le x_n$$ Attenzione!! Ricordati che è importante ordinare le modalità della variabile per calcolare correttamente il coefficiente di Gini.
Denotiamo con $A_i$ l'ammontare del carattere posseduto dalle $i$ unità più povere: $$A_i=x_1+x_2+\dots +x_i=\sum\limits_{j=1}^ix_j$$ e con $A$ l'ammontare totale del carattere di tutte le unità statistiche: $$A=x_1+x_2+\dots +x_n=\sum\limits_{j=1}^nx_j$$
Chiamiamo con $Q_i$ l'ammontare relativo del carattere posseduto dalle $i$ unità più povere e con $P_i$ l'ammontare relativo del carattere posseduto dalle $i$ unità più povere nel caso (ipotetico) di equidistribuzione: $$\begin{eqnarray} Q_i &=& \frac{A_i}{A}\\ P_i &=& \frac{i}{n}\end{eqnarray}$$
Allora la formula del rapporto di concetrazione di Gini è: $$\bbox[#ffffff,5px,border:2px solid #ff6600]{G=\cfrac{\sum\limits_{i=1}^{n-1}(P_i-Q_i)}{\sum\limits_{i=1}^{n-1}P_i}=1-\cfrac{\sum\limits_{i=1}^{n-1}Q_i}{\sum\limits_{i=1}^{n-1}P_i}}$$
In alternativa, è possibile calcolare l'indice di Gini usando una formula operativa che richiede meno calcoli e quindi più veloce da applicare $$\bbox[#ffffff,5px,border:2px solid #ff6600]{G=1-2\cdot\cfrac{\sum\limits_{i=1}^{n-1}Q_i}{n-1}}$$
In generale è possibile seguire la seguente tabella per interpretare il livello di concentrazione di Gini:
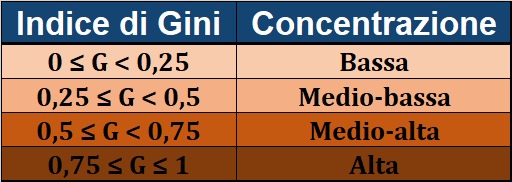
Ti consiglio di proseguire la lettura perché in fondo troverai un esempio numerico che ti farà capire meglio come calcolare l'indice di concentrazione di Gini. Inoltre, puoi cliccare sul bottone qui sotto per visualizzare altri esercizi svolti sull'indice di Gini. In particolare, te ne ho risolto uno in cui è necessario applicare una procedura di calcolo dell'indice di Gini specifica per le distribuzioni di frequenza in classi.
Proprietà dell'indice di concentrazione di Gini
- Diminuisce (aumenta) se tutti i valori della variabile vengono aumentati (diminuiti) di una stessa quantità positiva;
- è sensibile ai trasferimenti: se una parte del reddito di un individuo ricco viene trasferita a un individuo più povero l'indice diminuisce. Al contrario, se una parte del reddito viene trasferita da un individuo più povero a uno più ricco, l'indice aumenta.
- è invariante rispetto alle trasformazioni di scala dei redditi: non varia se si moltiplicano o si dividono tutti i redditi per una stessa quantità positiva.
Curva di Lorenz
Il livello di concentrazione di un fenomeno si può anche rappresentare graficamente mediante una curva chiamata curva di Lorenz. Non è altro che un grafico ottenuto unendo con dei segmenti i punti di coordinate $(P_i,Q_i)$, per $i=1,\dots , n$ che formano così una spezzata. La regione del piano delimitata dalla curca di Lorenz e dalla bisettrice indica la concentrazione del fenomeno: maggiore è tale area maggiore è la concentrazione.
Interpretazione dei punti del diagramma di Lorenz
Ti starai chiedendo cosa indicano i punti $(P_i,Q_i)$ calcolati e tracciati nel diagramma di Lorenz. Per facilitare la comprensione, supponiamo che la variabile in esame sia proprio il reddito. Allora:
- $P_i$ rappresenta la proporzione di popolazione che percepisce un reddito minore o uguale a $x_i$;
- $Q_i$ rappresenta la proporzione della ricchezza complessiva determinata dalla quota di proporzione $P_i$.
Ti presento un esempio numerico che ti chiarirà il tutto.
Esempio
Il capitale azionario di una società è suddiviso tra 7 soci nelle seguenti quantità: 25, 89, 106, 155, 223, 368, 509 per un totale di 1475 migliaia di euro.
- Calcolare il rapporto di concentrazione di Gini e commentare il risultato.
- Disegnare la curva di Lorenz sui dati, evidenziando l'area di concentrazione.
Innanzitutto, calcoliamo gli $A_i,Q_i$ e $P_i$ come dalle formule sopra. Tutti i calcoli vengono riportarti nella seguente tabella.

Una volta costruita la tabella soprastante è facile calcolare l'indice di concentrazione di Gini: $$\begin{array}{l}G=1-\cfrac{\sum\limits_{i=1}^{6}Q_i}{\sum\limits_{i=1}^{6}P_i}=\\1-\cfrac{1.5580}{3}=0.4807\end{array}$$
Applicando la formula operativa otteniamo lo stesso risultato: $$\begin{array}{l}G=1-2\cdot\cfrac{\sum\limits_{i=1}^{n-1}Q_i}{n-1}\\=1-2\cdot\cfrac{1,5580}{6}=0.4807\end{array}$$
Tale indice ci dice che c'è una notevole concentrazione e che quindi il capitale è nelle mani di pochi soci. Inoltre, possiamo commentare il generico punto di coordinate $(P_i;Q_i)$, ad esempio $(P_3;Q_3)$: il 42% circa dei soci più poveri, detiene quasi il 15% della ricchezza totale della popolazione.
Tracciando i punti $(P_i;Q_i)$, unendoli tramite una spezzata e disegnando la bisettrice del primo quadrante (ovvero la retta che congiunge l'origine al punto (1;1)), otteniamo la curva di Lorenz:
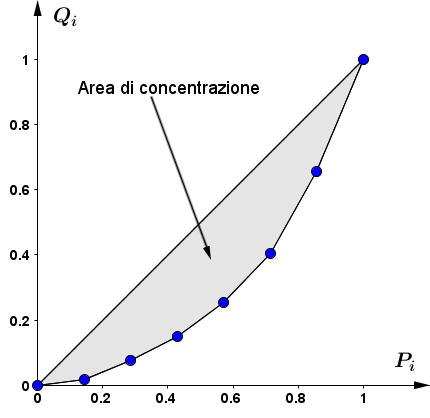
Come abbiamo già detto l'area di concentrazione è l'area compresa tra la spezzata che unisce i punti $(P_i;Q_i)$ e la bisettrice congiungente i punti $(0;0)$ e $(1;1)$.



