La regressione lineare è quella tecnica statistica utilizzata per studiare le relazioni che intercorrono tra due o più caratteri (variabili) statistici di cui una chiamata variabile dipendente e il resto sono chiamati regressori o variabili indipendenti. Infatti, lo scopo della regressione è quello di analizzare la dipendenza lineare tra le suddette variabili. Nel caso della regressione lineare semplice si studia la dipendenza lineare tra una variabile quantitativa numerica Y e una variabile numerica o dicotomica X. Tale studio consiste nello stimare dei coefficienti $b_0$ e $b_1$ tale che la retta $Y=b_0+b_1\cdot X$ sia la migliore interpolatrice delle coppie dei valori osservati $(x_i,y_i)$, essendo $x_i$ i valori assunti dalla variabile $X$ e $y_i$ i valori assunti dalla variabile $Y$. In che senso? Guarda il grafico qui sotto.

I punti verdi sono le coppie $(x_i,y_i)$ mentre la linea blu è la retta $Y=b_0+b_1\cdot X$. Osserva inoltre l'errore $\varepsilon_i$ che si commette approssimando il punto reale di ordinata $y_i$ con uno appartenente alla retta di ordinata inferiore (o superiore) $\hat{y}_i=y_i+\varepsilon_i$. $\hat{y}$ è chiamato y stimato o predetto dal modello $\hat{y}=b_0+b_1\cdot X$. Appare chiaro allora che la migliore retta la ottengo imponendo che le distanze tra i valori osservati $y_i$ e i valori teorici o predetti $\hat{y}_i$ siano le minime possibili. Su questo si basa il metodo dei minimi quadrati.
Metodo dei minimi quadrati e stima dei coefficienti della retta di regressione
Il metodo dei minimi quadrati consiste nel minimizzare le differenze $\hat{y}_i-y_i$ tra i punti osservati e quelli teorici e quindi trovare il best fit dei dati contenuti nelle variabili X e Y. Per far ciò si considerano le differenze al quadrato $(\hat{y}_i-y_i)^2$ in modo da evitare che differenze negative annullino l'effetto delle differenze positive. La quantità totale da minimizzare è dunque $$\begin{array}{l}\sum\limits_{i=1}^n(\hat{y}_i-y_i)^2=\\ \sum\limits_{i=1}^n(b_0+b_1\cdot x_i-y_i)^2\end{array}$$
Senza scendere nei dettagli (ma se vuoi approfondirlo mettiti in contatto con me) si calcolano le derivate di tale sommatoria rispetto a $b_0$ e $b_1$ e si pongono uguale a zero. Facendo alcuni passaggi algebrici si ottengono le formule per calcolare i parametri della retta di regressione lineare semplice $b_0$ e $b_1$:
$$\begin{array}{l}b_1=\cfrac{COV(X,Y)}{\sigma_x^2}\\ b_0=\overline{y}-b_1\overline{x}\end{array}$$ dove $COV(X,Y)$ è la covarianza tra X e Y, $\sigma_x^2$ è la varianza di X mentre $\overline{y}$ e $\overline{x}$ sono rispettivamente i valori medi di Y e di X.
Nota: Per il calcolo del valor medio e della varianza puoi consultare questo articolo, mentre per il calcolo della covarianza vai a questa lezione:
Passiamo adesso al significato statistico e geometrico dei parametri della retta di regressione.
La retta di regressione: descrizione dei coefficienti
Il coefficiente $b_0$ è detto intercetta e rappresenta il valore della variabile $Y$ quando $X=0$; mentre $b_1$ è chiamato coefficiente angolare o coefficiente di regressione o, ancora, pendenza della retta e rappresenta la variazione subita in media dal carattere $Y$ per effetto di un aumento unitario del carattere $X$.
Guarda il video a fondo pagina per capire meglio il concetto con un esempio concreto di regressione lineare fatto con il software statistico R studio.
Significato geometrico della regressione lineare
Il coefficiente di regressione può variare da $-\infty$ a $+\infty$:
- se $b_1 > 0$, la retta di regressione è crescente e il carattere $Y$ aumenta all'aumentare di $X$
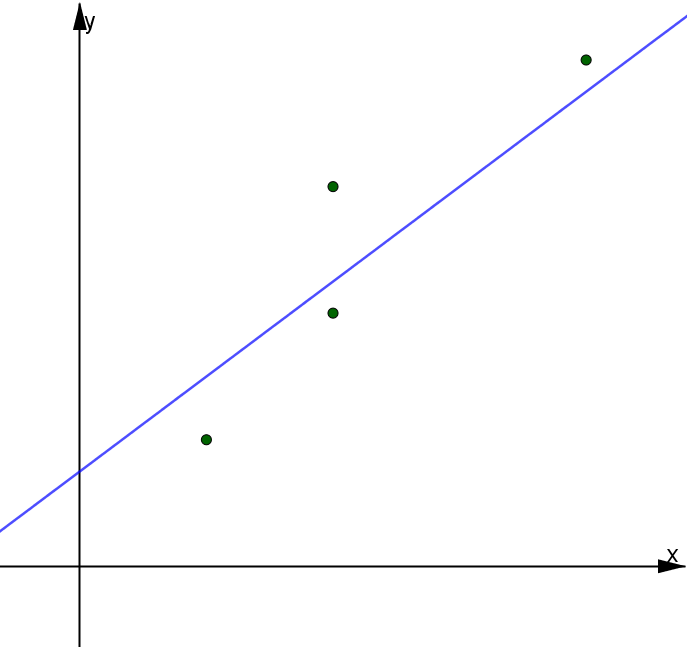
- se $b_1 < 0$, la retta di regressione è decrescente e il carattere $Y$ diminuisce all'aumentare di $X$

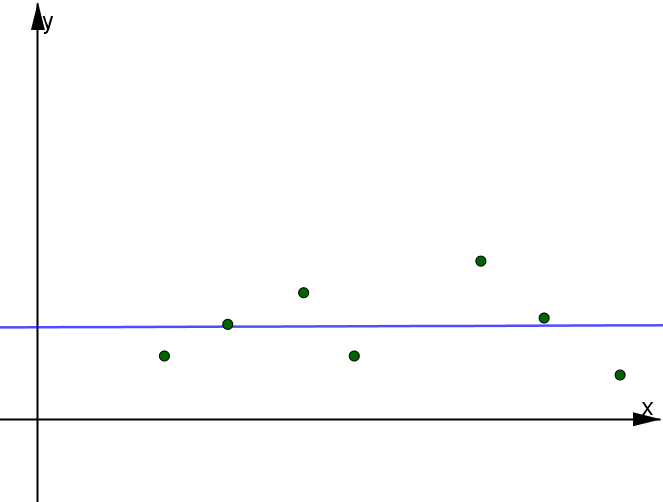
- se $b_1 = 0$, la retta di regressione è costante e il carattere $Y$ non varia al variare del carattere $X$
Legame tra regressione e correlazione lineare
Strettamente legata alla regressione è il concetto di correlazione, infatti:
- nella teoria della regressione lineare (semplice) si suppone che una variabile $X$ assume valori determinati e si cerca la relazione che lega la seconda variabile $Y$ alla prima: in altre parole si cerca di stabilire un legame funzionale tra le due variabili (del tipo $Y=b_0+b_1X$).
- nella teoria della correlazione si determina il grado di interdipendenza tra le due variabili, ovvero si determina se a una variazione del carattere $X$ corrisponde una variazione più o meno sensibile del carattere $Y$.
Bontà del modello di regressione: coefficiente di determinazione $R^2$
Per capire se il modello è buono, cioè si adatta bene ai dati (geometricamente i punti non si discostano tanto dalla retta). Si calcola il cosiddetto indice di determinazione $R^2$ detto anche indice della bontà di adattamento del modello. L'$R^2$ si calcola facendo il rapporto tra la devianza spiegata (o SSR) e la devianza totale (o SST) $$R^2=\cfrac{DEV_{spiegata}}{DEV_{totale}}= \cfrac{SSR}{SST}$$. Ti parlerò in dettaglio di queste due devianze nei paragrafi successivi perché mi voglio adesso focalizzare sul significato del coefficiente di determinazione.
L'$R^2$ è un indice che varia tra 0 e 1 e misura la quantità di informazione o variabilità della Y che la X riesce a spiegare. In parole semplice, più R si avvicina a 1 migliore sarà il modello; più invece si avvicina a 0 peggiore sarà il modello. Un modo alternativo per calcolare l'$R^2$ è mediante il coefficiente di correlazione di Pearson. Infatti, si dimostra che l'indice di determinazione è pari al coefficiente di correlazione di Pearson al quadrato: $$R^2=\rho^2$$ dove $$\rho=\cfrac{COV(X,Y)}{\sqrt{\sigma_x^2\cdot \sigma_y^2}}$$
Per approfondimenti vai alla lezione sul coefficiente di correlazione lineare $\rho$.
Da un punto di vista matematico maggiore è $R^2$ maggiore è la devianza spiegata e quindi maggiore sarà la proporzione di variabilità totale che la retta di regressione stimata riesce a spiegare.
Scomposizione della devianza
La devianza totale $DEV(Y)$ o $SST$ (acronimo di Sum Square Total) non è altro che la somma dei quadrati degli scarti tra i valori osservati $y_i$ e il valore medio $\overline{y}$.
$DEV_{totale}=SST=DEV(Y)=\sum\limits_{i=1}^n[y_i-\overline{y}]^2$
Mentre la devianza spiegata o di regressione $DEV_{spiegata}$ o $SSR$ (acronimo di Sum Square Regression) è la somma dei quadrati degli scarti tra i valori teorici $\hat{y}_i$ e il valore medio $\overline{y}$.
$DEV_{spiegata}=SSR=\sum\limits_{i=1}^n[\hat{y}_i-\overline{y}]^2$
Ti faccio osservare che puoi ricavare la varianza totale di Y (detta anche varianza del modello) facendo il rapporto tra devianza totale e il numero totale $n$ di osservazioni $$\sigma_y^2=VAR(Y)=\cfrac{DEV(Y)}{n}$$
Inoltre possiamo definire la devianza residua $DEV_{residua}$ o $SSE$ (acronimo di Sum Square Error) come la somma dei quadrati degli errori che si commettono approssimando il valore osservato $y_i$ con il valore teorico $\hat{y}_i$. La varianza residua o stima della varianza della popolazione, sarà invece $$VAR_{residua}=\frac{DEV_{residua}}{n-2}$$
Si può dimostrare che la devianza totale (come pure la varianza totale) si può decomporre nella somma delle altre due devianze, ossia: $$DEV_{totale}=DEV_{spiegata}+DEV_{residua}$$
Regressione lineare semplice in Excel
Excel è un ottimo strumento per semplificare i suddetti calcoli della regressione lineare specialmente quando il numero di osservazioni contenute nel tuo dataset è elevato. A questo proposito, ho predisposto un file Excel in cui ho calcolato tutte quelle misure necessarie ai fini di uno studio completo di un modello di regressione lineare semplice. Clicca nel bottone qui in basso per scaricare il file.
Regressione lineare semplice in R
Nel video ti spiego quali sono i comandi R necessari per condurre un'analisi di regressione lineare semplice e come interpretare i risultati.



