La distribuzione esponenziale si utilizza generalmente per numeri aleatori il cui significato è il tempo di durata fino al guasto di un certo dispositivo. Sto ovviamente parlando di una distribuzione di variabile continua. Di seguito ti descrivo la distribuzione di probabilità di una variabile esponenziale e le principali caratteristiche.
Funzione di densità e di ripartizione della distribuzione esponenziale
Una variabile aleatoria $X$ ha distribuzione esponenziale di parametro $\lambda$ e si indica con $X\sim EXP(\lambda)$, se la sua funzione di densità è
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{f(x)=\begin{cases} \lambda e^{-\lambda x}&\mbox{se } x > 0\\ 0 &\mbox{se } x\le 0\end{cases}}$$
Inoltre, integrando la funzione di densità
$$F(x)=P(X\le x)=\begin{cases} \int_0^x\lambda e^{-\lambda t}\ dt&\mbox{se } x > 0\\ 0 &\mbox{se } x\le 0\end{cases}$$
si ottiene la sua funzione di ripartizione o cumulata:
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{F(x)=P(X\le x)=\begin{cases} 1-e^{-\lambda x}&\mbox{se } x > 0\\ 0 &\mbox{se } x\le 0\end{cases}}$$
Funzione di sopravvivenza della distribuzione esponenziale
$F(x)=P(X\le x)$ rappresenta la probabilità che il dispositivo si guasti nell'intervallo $[0,x]$. La funzione contraria, chiamata funzione di sopravvivenza e indicata con $S(x)=P(X > x)$, è invece la probabilità che il dispositivo si guasti dopo l'istante di tempo $x$.
Dunque la funzione di sopravvivenza di una variabile esponenziale è definita come:
$$S(x)=1-F(x)=e^{-\lambda x}$$
Valore atteso e varianza di una distribuzione esponenziale
Applicando le definizione di valore atteso e varianza di un numero aleatorio continuo si può facilmente verificare che, se $X\sim EXP(\lambda)$, risulta:
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{E(x)=\frac{1}{\lambda}}$$
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{VAR(X)=\frac{1}{\lambda^2}}$$
Proprietà di assenza di memoria
Si può dimostrare che per il numero aleatorio $X\ge 0$ con distribuzione esponenziale vale la proprietà di assenza di memoria:
$$P(X > x+x_0|X>x)=P(X > x_0)$$
Al primo membro dell'uguaglianza abbiamo la probabilità che il dispositivo si guasti dopo l'istante $x+x_0$, supposto che non si sia guastato fino all'istante $x$. Mentre al secondo membro c'è la probabilità che il dispositivo si guasti dopo l'istante $x_0$. Dunque, tale uguaglianza ci dice che man mano che il dispositivo viene utilizzato, la probabilità di guastarsi non cambia ed è sempre uguale alla probabilità di non guastarsi fino al tempo $x_0$.
In altre parole, per la proprietà di assenza di memoria, si ha che ogni variabile aleatoria con distribuzione esponenziale rappresenta il tempo di durata fino al guasto di un dispositivo ideale che non è soggetto a usura.
Funzione di rischio
È chiaro che, in generale, un dispositivo si usura, quindi si ha invecchiamento quando
$$P(X\le x+\delta x|X>x)>P(X\le\delta x)$$
In opposizione a questa, diremo che si ha ringiovanimento quando si verifica che
$$P(X\le x+\delta x|X>x)< P(X\le\delta x)$$
Da quest'ultima si ha che:
$$P(X\le x+\delta x|X>x) = \frac{P(x < X\le x+\delta x)}{P(X > x)}\simeq\frac{\delta x f(x)}{S(x)}$$
Infatti, $S(x)=P(X > x)$ che è la funzione di sopravvivenza; mentre al numeratore, considerando un piccolo incremento di $x$, $P(x < X\le x+\delta x)$ non è altro che l'area sottesa dalla $f(x)$ nell'intervallo in figura:
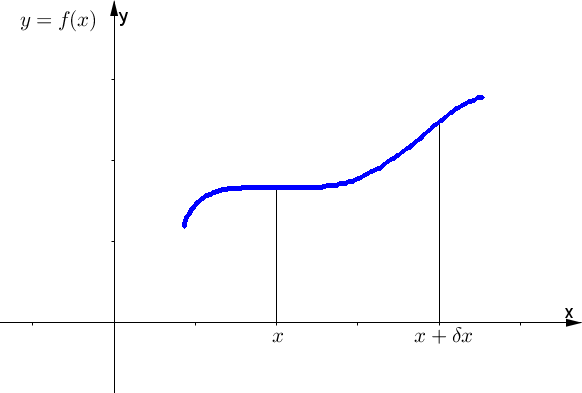
Se l'incremento è molto piccolo, tale area si può ben approssimare con quella del rettangolo di base $\delta x$ e altezza $f(x)$.
Chiamiamo funzione di rischio il rapporto tra la funzione di densità $f(x)$ e la funzione di sopravvivenza $S(x)$:
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{h(x)=\frac{f(x)}{S(x)}}$$
Ovviamente
- se $h(x)$ è crescente $\Rightarrow$ invecchiamento
- se $h(x)$ è decrescente $\Rightarrow$ ringiovanimento.
La funzione di rischio per un numero aleatorio con distribuzione esponenziale, è chiaramente costante:
$$h(x)=\frac{\lambda e^{-\lambda x}}{e^{-\lambda x}}=\lambda$$
Affinché $h(x)$ sia una funzione di rischio devono essere verificate le seguenti proprietà:
- $h(x)\ge 0\ \forall x\ge 0$
- $S(+\infty)=\int_0^{+\infty}h(t)\ dt = +\infty$



