Fissati un punto $O$ nel piano e un numero reale $k\neq 0$, l'omotetia è la trasformazione geometrica che a un punto $P$ fa corrispondere il punto $P'$ tale che $P'$ appartiene alla retta $OP$ e $\frac{OP'}{OP}=k$.
Il punto $O$ è detto centro dell'omotetia e $k$ rapporto di omotetia.
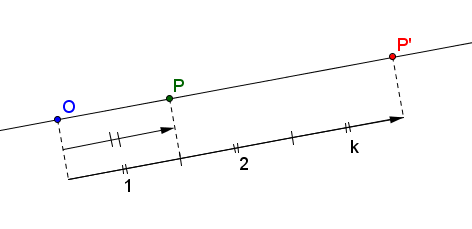
Le equazioni che descrivono un omotetia di centro l'origine $O$ degli assi cartesiani sono:
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{\begin{cases} x'=kx\\ y'=ky\end{cases}}$$
Nel caso in cui si abbia un'omotetia di centro $C(x_0,y_0)$ differente dall'origine, le equazioni diventano:
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{\begin{cases} x'=kx+x_0(1-k)\\ y'=ky+y_0(1-k)\end{cases}}$$
Alcuni casi particolari di omotetia:
- Se $k > 0$ l'omotetia si dice diretta;
- Se $k < 0$ l'omotetia si dice inversa;
- Se $k = 1$ si ha una identità;
- Se $k = -1$ si ha una una simmetria centrale.
Si può dimostrare che l'omotetia gode delle seguenti proprietà:
- in una omotetia di rapporto $k$, a un segmento $AB$ corrisponde un segmento $A'B'$ parallelo ad $AB$ e tale che $\frac{A'B'}{AB}=k$;
- in una omotetia a ogni angolo corrisponde un angolo congruente;
- l'omotetia è una similitudine;
- le rette che passano per il centro di omotetia sono rette unite;
- se $k\neq 1$ il centro di omotetia è l'unico punto unito.



