In questa lezione introduciamo lo studio delle sezioni coniche descrivendo come esse si generano. Innanzitutto, diamo qualche cenno storico.
Le sezioni coniche nascono dall'esigenza degli scienziati di estendere i concetti di geometria euclidea, quali rette e cerchi, a figure più complesse, come ellissi, parabole e iperboli che descrivevano ad esempio le traiettorie dei pianeti, delle comete e dei proiettili, la rifrazione dei raggi luminosi attraverso dei materiali, il funzionamento di lenti, telescopi e perfino dell'occhio umano. Queste necessità spinsero i matematici a sviluppare la geometria delle coniche.
Ma come si generano queste coniche e che forma hanno?
Prendiamo una superficie generata dalla rotazione completa di una retta generatrice $g$ attorno a un'asse $a$, incidente con la prima nel vertice $V$ e formante un angolo di semiapertura $\alpha$. Si ottiene così una superficie conica a due falde (vedi figura)
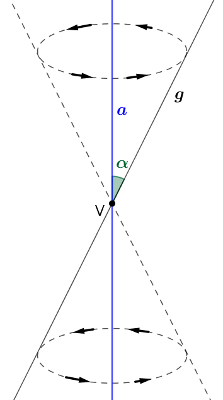
Intersechiamo ora la superficie con un piano non passante per il vertice. A seconda dell'inclinazione del piano rispetto l'asse, si ottengono le diverse coniche.
In particolare, se il piano interseca il cono formando con l'asse un angolo $\beta$ uguale all'angolo $\alpha$, si ottiene una parabola

Se invece il piano interseca la superficie conica formando un angolo $\beta=90°$ con l'asse, otteniamo una circonferenza:

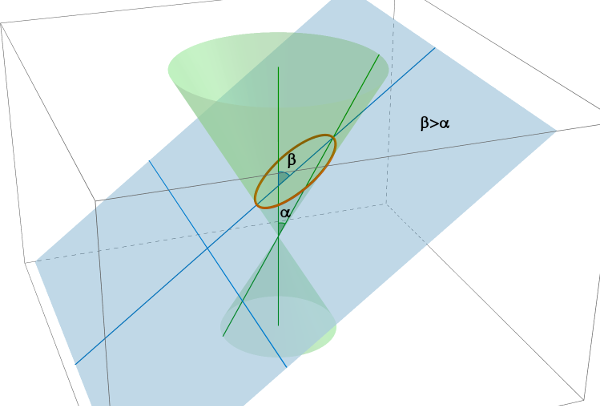
Se l'angolo $\beta$ di inclinazione è maggiore dell'angolo $\alpha$, allora si ottiene un'ellisse:
infine, se $\beta < \alpha$ si generano i due rami di iperbole:




