In questa lezione daremo la definizione di parabola come luogo geometrico e impareremo come disegnarla e trovare gli elementi che la caratterizzano.
La parabola è il luogo dei punti del piano equidistanti da una retta fissa, detta direttrice, e da un punto fisso, detto fuoco. Per capire tale definizione diamo uno sguardo alla figura sottostante.

Preso arbitrariamente un punto $P_1$ sulla parabola, la sua distanza dal fuoco $F$ è uguale alla distanza dalla direttrice $d$. Guardando la figura, si ha $\overline{P_1F}=\overline{P_1H_1}$. Tale proprietà è verificata per qualsiasi punto scelto sulla parabola (vedi, ad esempio i punti $P_2$ e $P_3$).
La retta passante per il fuoco $F$ e perpendicolare alla direttrice $d$ è chiamata asse di simmetria della parabola. Il nome è dovuto al fatto che a ogni punto $P$ del luogo corrisponde un punto $P'$, a esso simmetrico rispetto a tale asse, anch'esso equidistante dal fuoco e dalla direttrice (vedi ad esempio i punti $P'_1$, $P'_2$ e $P'_3$).
Equazione della parabola
Ci sono due possibili equazioni della parabola:
- l'equazione della parabola con asse di simmetria verticale, ossia parallelo all'asse y ($y=ax^2+bx+c$)
- l'equazione della parabola con asse di simmetria orizzontale, ossia parallelo all'asse x ($x=ay^2+by+c$)
Descriveremo in dettaglio la prima, dando le formule per il calcolo degli elementi importanti della parabola. Se sei interessato al secondo tipo vai avanti.
Consideriamo l'equazione generica di una parabola con asse di simmetria verticale: $$\bbox[#ffffff,5px,border:2px solid #ff6600]{y=ax^2+bx+c}$$ dove a, b e c sono numeri reali con $a\neq 0$ (se a=0 l'equazione è quella di una retta).
Il segno del coefficiente a di $x^2$ indica la concavità della parabola che può essere verso il basso o verso l'alto. Come mostra la figura in basso, se $a>0$ la concavità della parabola è verso l'alto (sorride); viceversa, se $a < 0$, la concavità è verso il basso (piange).

Per disegnare una parabola sul piano cartesiano abbiamo essenzialmente bisogno di trovare le coordinate del vertice e le intersezioni con gli assi x e y. Le coordinate del vertice della parabola sono date da $$\bbox[#ffffff,5px,border:2px solid #ff6600]{V=\left(-\frac{b}{2a},-\frac{\Delta}{4a}\right)}\quad (1)$$ dove ricordiamo $\Delta=b^2-4ac$ è il discriminante o Delta visto nelle equazioni di secondo grado.
Le intersezioni della parabola con l'asse x (che ha equazione y=0) si trovano risolvendo il seguente sistema: $$\begin{cases} y=ax^2+bx+c\\ y=0\end{cases}$$ che equivale a trovare le radici dell'equazione di secondo grado $ax^2+bx+c=0$
Mentre invece, le intersezioni della parabola con l'asse y si trovano intersecando l'equazione della parabola con quella dell'asse y (x=0): $$\begin{cases} y=ax^2+bx+c\\ x=0\end{cases}$$
Per risolvere quest'ultimo sistema basta sostituire 0 al posto della x nell'equazione della parabola ottenendo $y=c$. Dunque, il punto $(0,c)$ sarà il punto di intersezione con l'asse verticale.
Esempio
Supponiamo di voler disegnare la parabola di equazione $y=x^2-5x+4$
Osservando che $a=1$, $b=-5$ e $c=4$, calcoliamo il Delta: $$\Delta=(-5)^2-4\cdot 1\cdot 4=9$$
Calcolando il vertice usando la formula data (1) otteniamo $$V=\left(\frac{5}{2},-\frac{9}{4}\right)$$
Troviamo i punti di intersezione della parabola con l'asse x risolvendo l'equazione $x^2-5x+4=0$ con la formula del delta: $$x=\frac{5\pm\sqrt{9}}{2}=\begin{array}{l} \nearrow\\ \searrow\end{array} \begin{array}{l} 4 \\ \\ 1\end{array}$$
Abbiamo così ottenuto i punti $A=(1,0)$ e $B=(4,0)$.
L'intersezione con l'asse y è banalmente $C=(0,4)$
Congiungendo i punti trovati incluso il vertice, otteniamo il grafico della parabola data: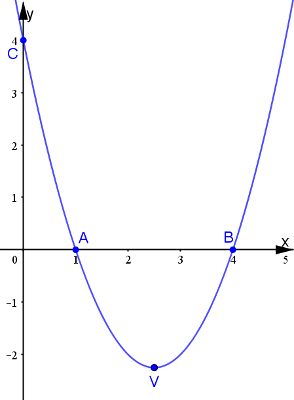
Relazione tra segno del delta e intersezioni della parabola con l'asse x
Mediante il calcolo del delta possiamo stabilire a priori la posizione della parabola rispetto all'asse x ed, in particolare, quanti sono i punti di intersezione con l'asse x. Si possono verificare tre situazioni differenti:
- se $\Delta >0$ la parabola interseca l'asse x in due punti distinti $x_1$ e $x_2$.
- se $\Delta = 0$ la parabola interseca l'asse x in un solo punto, il vertice (il quale giace appunto sull'asse x).
- se $\Delta < 0$ la parabola non interseca l'asse x (la parabola si trova completamente sopra oppure completamente sotto l'asse x.
Il grafico qui sotto sintetizza quanto detto.
Come già menzionato sopra, un altro elemento che caratterizza la parabola è l'asse di simmetria. Essa ha equazione $$\bbox[#ffffff,5px,border:2px solid #ff6600]{x=-\frac{b}{2a}}\quad (2)$$
Molto semplicemente si può trovare anche l'equazione della direttrice: $$\bbox[#ffffff,5px,border:2px solid #ff6600]{y=-\frac{1+\Delta}{4a}}\quad (3)$$ e le coordinate del fuoco: $$\bbox[#ffffff,5px,border:2px solid #ff6600]{F=\left(-\frac{b}{2a},\frac{1-\Delta}{4a}\right)}\quad (4)$$
La parabola con asse di simmetria orizzontale
L'equazione della parabola in questo caso si ottiene scambiando la x con la y: $$\bbox[#ffffff,5px,border:2px solid #ff6600]{x=ay^2+by+c}$$ dove stavolta il segno del coefficiente $a$ indica se la parabola è orientata verso destra ($a>0$) o sinistra ($a<0$) come mostra l'immagine qui sotto.
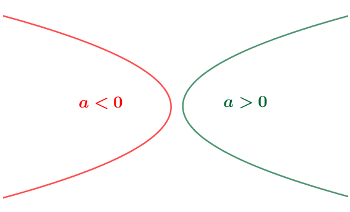
Analogamente a quanto fatto per la parabola con asse di simmetria verticale, riassumiamo le formule necessarie per lo studio della parabola con asse di simmetria orizzontale:
- Coordinate del vertice: $\large{V=\left(-\frac{\Delta}{4a},-\frac{b}{2a}\right)}$
- Coordinate del fuoco: $\large{F=\left(\frac{1-\Delta}{4a},-\frac{b}{2a}\right)}$
- Equazione dell'asse di simmetria: $\large{y=-\frac{b}{2a}}$
- Equazione della direttrice: $\large{x=-\frac{1+\Delta}{4a}}$




