Le onde periodiche sono quelle onde che avanzano lungo l'asse x formando delle ripetizioni regolari di oscillazioni sinusoidali, ciascuna delle quali ha la stessa lunghezza L e si completa in un certo tempo T (più avanti vedremo che T rappresenta il periodo dell'onda periodica).
Per visualizzare il profilo dell'onda si fissa il tempo t e si disegna il grafico di y in funzione di x come mostra l'immagine qui sotto:
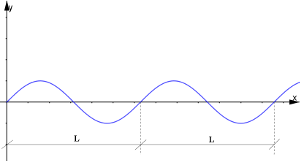
Osservazione
Facciamo osservare che il profilo dell'onda è sinusoidale solo se l'onda è di tipo armonico, ossia generata da una sorgente che oscilla di moto armonico.
Altre due distanze che caratterizzano le onde periodiche sono l'ampiezza e la lunghezza d'onda.
La lunghezza d'onda $\lambda$ è la distanza tra due creste o due gole successive, mentre l'ampiezza dell'onda è il valore massimo di y raggiunto dal profilo dell'onda.
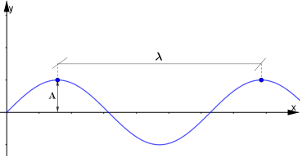
Adesso, fissiamo un punto x lungo la direzione di propagazione di un'onda periodica e osserviamo come esso si muove al trascorrere del tempo: mentre l'onda si sposta in orizzontale, il punto oscilla su e giù. Inoltre, la grandezza y che descrive l'onda oscilla con moto periodico nel tempo. L'intervallo di tempo impiegato da y per compiere un'oscillazione completa è chiamato periodo T dell'onda.

Definiamo frequenza f il numero di oscillazioni che, nel punto x fissato, l'onda compie in 1 secondo ed è data dato dall'inverso del periodo. L'unità di misura della frequenza è l'Herz (in simboli Hz). $$\bbox[#ffffff,5px,border:2px solid #ff6600]{f=\frac{1}{T}\ [Hz]\quad (\large{1})}$$
La velocità di propagazione di un'onda è la velocità con cui l'onda percorre la distanza di una lunghezza d'onda nell'intervallo di tempo di un periodo: $$\bbox[#ffffff,5px,border:2px solid #ff6600]{v=\frac{\lambda}{T}=\lambda\cdot f\quad (\large{2})}$$
Chiaramente la velocità di propagazione dipende dal tipo di mezzo di trasmissione dell'onda.
Velocità di propagazione lungo una corda tesa
La velocità v di una corda tesa dipende dalla forza di tensione $F_T$ e dalla densità lineare $d_L$ della corda ed è data da $$v=\sqrt{\frac{F_T}{d_L}}$$
Questo ci dice che maggiore è la tensione della corda, maggiore sarà la velocità; di contro, maggiore è la densità lineare e minore sarà la velocità.
Possiamo dire che, in generale, la velocità di propagazione di un'onda meccanica è la radice quadrata del rapporto fra una quantità che misura l'elasticità del mezzo (la tensione della corda $F_T$) e un'altra che ne misura l'inerzia (la densità della corda $d_L$).
Velocità di propagazione lungo una sbarra solida
Usando la generalizzazione appena introdotta, possiamo ricavare la velocità di un'onda meccanica che si propaga lungo una sbarra solida omogenea mediante la formula: $$v=\sqrt{\frac{e}{d}}$$
Dove $e$ è il coefficiente caratteristico del materiale di cui è costituita la sbarra e $d$ è la densità della sbarra (data dal rapporto fra massa e volume).
Velocità di propagazione attraverso un fluido
Analogamente, per un'onda longitudinale che attraversa un fluido di densità $d$: $$v=\sqrt{\frac{b}{d}}$$
Dove $b$ è detto modulo di compressione.
Profilo di un'onda in termini di spostamento e velocità
Per visualizzare il concetto di propagazione di un'onda in termini di velocità e spostamento immaginiamo di avere un'onda con fase iniziale $\phi_0=0$ e consideriamo la ($\large\star\large\star$). Quello che avviene fisicamente è descritto dalla figura in basso:
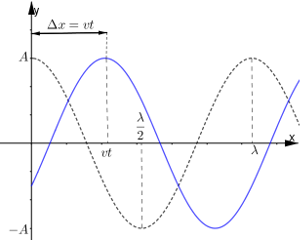
Se l'onda si propaga con velocità v, nell'instante t il suo profilo si è spostato in avanti, rimanendo uguale a se stesso di un tratto $\Delta x=vt$. Il primo massimo (A), che ora corrisponde alla coordinata $x=vt$, inizialmente corrispondeva alla coordinata 0.
Vai alla prossima lezione (sulle onde armoniche) per approfondire il concetto dando uno sguardo alle equazioni delle onde espresse in funzione di spostamento, tempo e velocità.



