Dopo aver parlato in generale di onde periodiche, approfondiamo il concetto di onda descrivendo le equazioni che definiscono onde armoniche come particolare tipo di onda periodica.
Tale trattazione va fatta descrivendo i diversi tipi di equazione di un onda che muta espressione a seconda della variabile che varia:
- Equazione delle onde armoniche fissato un punto x (equazione in funzione del tempo).
- Equazione delle onde armoniche in un istante fissato t (equazione in funzione della posizione x).
- Equazione delle onde armoniche al variare del punto x e del tempo t.
- Equazione delle onde armoniche espressa con il numero d'onda.
Legge delle onde armoniche in un punto fissato
Particolari onde periodiche sono le onde armoniche. La legge temporale dello spostamento y di un punto fissato sulla corda è data da: $$\bbox[#ffffff,5px,border:2px solid #ff6600]{y=A\cos\left(\frac{2\pi}{T}t+\phi_0\right)=A\cos(\omega t+\phi_0)}\quad (\large\star)$$
dove:
- $A$ è l'ampiezza dell'onda;
- $T$ è il periodo;
- $\omega=\frac{2\pi}{T}$ è la pulsazione del moto armonico espressa in $\frac{rad}{s}$;
- l'argomento della funzione coseno $\omega t+\phi_0$ è la fase del moto espressa in radianti;
- $\phi_0$ è la fase iniziale, ossia il valore della fase all'istante $t=0s$.
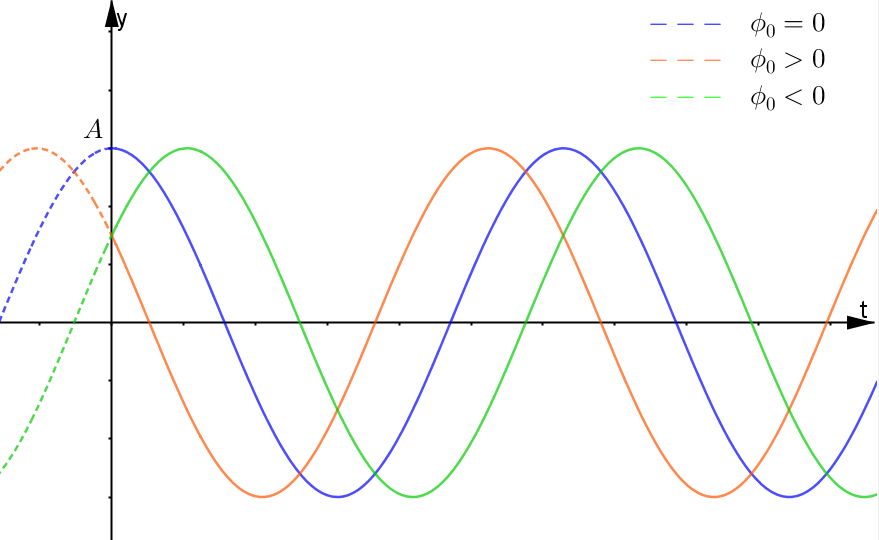
Nell'immagine sottostante vediamo tre onde con tre diverse fasi.
Quando la fase iniziale $\phi_0$ è 0 (onda blu), il punto della corda all'istante $t=0$ è esattamente a quota massima $A$.
Se la fase è positiva (onda arancione) o negativa (onda verde) l'onda appare traslata rispettivamente verso destra o verso sinistra.
Possiamo dunque dire che la fase iniziale è una costante che tiene conto delle condizioni iniziali dell'oscillazione.
Legge delle onde armoniche in un istante fissato
Avendo studiato lo spostamento y di un punto fissato al variare del tempo per un'onda armonica, descriviamo adesso come, fissato un istante di tempo t, il profilo di un'onda (lo spostamento y) varia al variare della posizione x lungo la corda.
In generale, l'equazione dello spostamento dell'onda al variare della posizione x è data da: $$\bbox[#ffffff,5px,border:2px solid #ff6600]{y=A\cos\left(\frac{2\pi}{\lambda}x+\phi_0\right)}\quad (\large\star\large\star)$$ dove $\lambda$ è la lunghezza d'onda e $\frac{2\pi}{\lambda}x+\phi_0$ costituisce la fase dell'onda come visto nella ($\large\star$). Qui la fase iniziale $\phi_0$ è il valore della fase nell'origine degli assi cartesiani, cioè per $x=0$
Legge delle onde armoniche al variare di x e t
La ($\large\star$) e ($\large\star\large\star$) esprimono la funzione spostamento separatamente al variare di x e t. E' possibile ricavare una formula più generale che esprime l'andamento dell'onda al variare sia di x sia di t.
Tale formula è chiamata funzione d'onda armonica ed è data da: $$\bbox[#ffffff,5px,border:2px solid #ff6600]{y=A\cos\left(\frac{2\pi}{\lambda}(x-vt)+\phi_0\right)}\quad (\large\star\large\star\large\star)$$ dove $\frac{2\pi}{\lambda}(x-vt)+\phi_0$ dipende da x e t e contiene la velocità di propagazione v dell'onda, cioè la grandezza che indica di quanto avanza l'onda nello spazio al trascorrere del tempo. La fase iniziale $\phi_0$ è il valore che assume la fase per t=0 e x=0.
Ricordando che $v=\frac{\lambda}{T}$ si ha pure che $\frac{v}{\lambda}=\frac{1}{T}$, allora la fase dell'onda soprascritta si può riscrivere come: $$\begin{eqnarray*} &=&\frac{2\pi}{\lambda}(x-vt)+\phi_0 \\ &=& \frac{2\pi}{\lambda}x-2\pi \frac{v}{\lambda}t+\phi_0 = \\ &=& \frac{2\pi}{\lambda}x-\frac{2\pi}{T}t+\phi_0 \end{eqnarray*}$$
Quindi, una forma equivalente della ($\large\star\large\star\large\star$) è $$y=A\cos\left(\frac{2\pi}{\lambda}x-\frac{2\pi}{T}t+\phi_0\right)\quad (\triangle)$$
Le formule enunciate in questo articolo valgono non solo per le onde armoniche lungo una corda ma anche per onde armoniche di altro tipo: ciò che cambia è il significato della variabile y.
Ad esempio, per un'onda che si propaga lungo una sbarra d'acciaio, la grandezza y che oscilla è la variazione di densità del materiale; per un'onda sonora, y può essere la variazione di pressione; per un'onda radio, il valore del campo elettrico.
Legge delle onde armoniche con il numero d'onda
Esiste una terza forma con cui la funzione d'onda può essere scritta. Prima di mostrarla, però, bisogna definire la pulsazione e il numero d'onda.
La pulsazione $\omega$ di un'onda armonica descrive la periodicità dell'onda nel tempo: $$\omega=\frac{2\pi}{T}\quad (1)$$
Essa coincide con la pulsazione del moto armonico compiuto da ciascun punto del mezzo attraverso cui l'onda si propaga.
Analogamente, il numero d'onda $\kappa$ descrive la periodicità dell'onda nello spazio attraverso la relazione: $$\kappa=\frac{2\pi}{\lambda}\quad (2)$$
Inoltre, ricondando che $v=\frac{\lambda}{T}$ abbiamo: $$v=\frac{\lambda}{T}\quad\rightarrow\quad \lambda=vT$$ da cui possiamo riscrivere il numero d'onda in funzione della pulsazione $\omega$ tenendo conto di (1) e (2): $$\begin{eqnarray*} \kappa &=&\frac{2\pi}{\lambda}=\frac{2\pi}{vT}=\\ &=&\frac{1}{v}\cdot\frac{2\pi}{T}=\frac{\omega}{v} \end{eqnarray*}$$ ossia $$\kappa=\frac{\omega}{v}\quad \bigg[\frac{rad}{m}\bigg]$$
Scriviamo quindi la funzione d'onda ($\triangle$) in funzione del numero d'onda $\kappa$ e della pulsazione $\omega$: $$\begin{eqnarray*} y &=& A\cos\left(\frac{2\pi}{\lambda}x-\frac{2\pi}{T}t+\phi_0\right)=\\ &=& A\cos(\kappa x -\omega t +\phi_0)\end{eqnarray*}$$ ovvero $$y=A\cos(\kappa x -\omega t +\phi_0)$$
Stavolta l'espressione della fase è: $$\phi=\kappa x-\omega t$$