In questo articolo vediamo come si passa da un ordine di grandezza a un altro di una stessa unità di misura. Pensiamo ad esempio al grammo. Vogliamo studiare come convertire una grandezza espressa in grammi a una espressa, ad esempio, in chilogrammi o in milligrammi. La prima cosa da fare è sicuramente fare un piccolo schema dei multipli e sottomultipli del grammo.
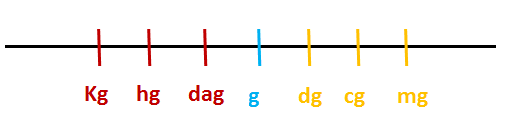
Nell'articolo precedente La misura e le unità fondamentali abbiamo visto le abbreviazioni e il significato dei simboli appena usati. Nell'immagine riportata sopra leggiamo a destra dei grammi i suoi primi tre sottomultipli (decigrammi, centigrammi, milligrammi) e a sinistra i suoi primi tre multipli (decagrammi, ettogrammi, chilogrammi). Chiaramente lo schema potrebbe essere esteso ad altri multipli e sottomultipli oppure usando un'altra unità di misura (ad esempio il metro, il secondo, ecc..).
Ritorniamo, quindi, al problema iniziale e supponiamo di voler convertire $1$ grammo in chilogrammi. Ci posizioniamo dunque sulla misura di partenza, cioè il grammo, e ci spostiamo verso la misura di arrivo, ovvero il chilogrammo. Per andare dal grammo al chilogrammo abbiamo fatto tre passi (ogni stanghetta è un passo) verso sinistra. Ogni passo verso sinistra equivale a moltiplicare per $10^{-1}$. Avendo quindi fatto tre passi a sinistra dovremo moltiplicare per $10^{-3}$ la misura da voler convertire. Nel caso specifico:
$$ 1 g = 1 \cdot 10^{-3} Kg = 0.001 Kg$$
Osserviamo che moltiplicare un qualsiasi numero per $10^{-1}$ equivale a dividere per $10$. Quindi nell'esempio di prima, visto che i passi da fare sono 3, divideremo per $1000$ la misura iniziale da convertire, pervenendo allo stesso risultato.
$$ 1 g= 1 \cdot 10^{-3} Kg = 1 \cdot \frac{1}{1000} Kg = 0.001 Kg$$

Se la quantità di grammi da convertire non è $1$ ma è qualsiasi numero basta fare lo stesso procedimento dove al posto di $1$ metteremo il nuovo numero da convertire. Ad esempio:
$$200 gr = 200 \cdot 10^{-3} Kg = 200 \cdot \frac{1}{1000} = 0.2 Kg $$
Osserviamo che usare le proprietà delle potenze di 10 agevola di molto i passaggi (per le proprietà delle potenze clicca qui). Infatti, nell'esempio precedente:
$$200 gr = 200 \cdot 10^{-3} Kg = 2 \cdot 10^{2} \cdot 10^{-3} Kg = 2 \cdot 10^{-1} Kg = \frac{2}{10} Kg = 0.2 Kg$$
Altri esempi di questo tipo potrebbero essere:
$$3 mg = 3 \cdot 10^{-2} dg = \frac{3}{100} dg = 0.03 dg $$
Per passare da milligrammi a decigrammi dobbiamo infatti spostarci di due passi a sinistra e quindi moltiplicare per $10^{-2},$ ovvero dividere per $100$.
$$50 cg = 50 \cdot 10^{-4} hg = 5 \cdot 10 \cdot 10^{-4} hg = 5 \cdot 10^{-3} hg = \frac{5}{1000} hg = 0.005 hg $$
Per passare da centigrammi a ettogrammi dobbiamo, infatti, spostarci di 4 passi a sinistra e moltiplicare quindi per $10^{-4}$.
Supponiamo, infine, di dover operare una conversione di ordine di grandezza per la quale dovremo spostarci verso destra. Come sarà facile intuire, questa volta si dovrà moltiplicare per potenze positive di $10$ il numero da voler convertire, tante volte quanti sono i passi da fare per raggiungere la misura finale.
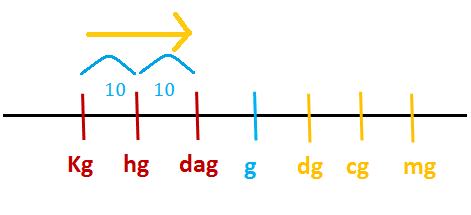
Ad esempio supponiamo di voler sapere a quanti decagrammi equivale un chilogrammo. Facendo riferimento sempre alla stessa immagine, ci posizioniamo sull'unità di misura iniziale (chilogrammi) e ci spostiamo di passo in passo (cioè di stanghetta in stanghetta) verso l'unità di misura finale (cioè i decagrammi). Nel caso specifico dovremo fare due passi e quindi dovremo moltiplicare per $10^2$.
$$ 1 Kg = 1 \cdot 10^2 dag = 100 dag $$
Anche in questo caso possiamo chiaramente convertire qualsiasi quantità diversa da 1. Ad esempio: $$20 g = 20 \cdot 10^3 mg = 2 \cdot 10 \cdot 10^3 mg = 2 \cdot 10^4 mg = 20000 mg$$ in quanto per passare da grammi a milligrammi mi sposto di tre passi verso destra. Oppure ancora:
$$25 hg = 25 \cdot 10^3 dg = 25000dg $$ infatti per andare da ettogrammi a decigrammi camminiamo di tre passi verso destra.



