Il test del chi-quadro di adattamento, (in inglese Goodness-of-fit-test) serve per valutare la bontà di adattamento dei dati campionari a una distribuzione teorica confrontando le frequenze empiriche o osservate, e le frequenze teoriche. Fai attenzione a non confonderlo con il test di ipotesi sull'indipendenza che ti ho spiegato in una lezione precedente (clicca nel link!).
Le ipotesi del test possono essere formulate come segue: $$\begin{cases} H_0: & \mbox{I dati si adattano alla distribuzione teorica}\\ H_1: & \mbox{I dati non si adattano alla distribuzione teorica}\end{cases}$$
Indicando con
- $X$ la variabile aleatoria con distribuzione di probabilità da sottoporre a verifica
- $k$ il numero delle modalità o dei valori assunti dalla variabile $X$
- $n_i,\ i=1\dots k$ le frequenze assolute osservate per ciascuna modalità
- $n$ la numerosità del campione o il totale delle frequenze assolute
- $\hat{p}_i,\ i=1\dots k$ le probabilità teoriche di ciascuna modalità
possiamo calcolare le frequenze teoriche o attese (nel caso l'ipotesi nulla fosse vera) per ciascuna modalità: $$\bbox[#ffffff,5px,border:2px solid #ff6600]{\hat{n_i}=n\cdot \hat{p}_i}$$
Attenzione! Per applicare correttamente il test occorre che nessuna frequenza teorica sia minore di 5. Quindi, se dal calcolo risulta che qualche frequenza teorica è minore di 5, bisogna raggruppare due o più modalità.
La statistica test da utilizzare è dunque la seguente: $$\bbox[#ffffff,5px,border:2px solid #ff6600]{\chi^2=\sum_{i=1}^k\cfrac{(n_i-\hat{n}_i)^2}{\hat{n}_i}}$$
In alternativa, puoi utilizzare la seguente formula operativa: $$\bbox[#ffffff,5px,border:2px solid #ff6600]{\chi^2=\sum_{i=1}^k\cfrac{n_i^2}{\hat{n}_i}-n}$$
La seguente tabella schematizza la procedura di calcolo del Chi-quadrato di adattamento:
A questo punto, dalle tavole della distribuzione chi-quadro, ricaviamo il valore critico con $\nu=k-1$ gradi di libertà e livello di significatività assegnato $\alpha$ e lo indichiamo con $\chi_{\nu,\ \alpha}^2$.
L'esito del test è: rifiuto $H_0$ se $\chi^2\geq\chi_{\nu,\ \alpha}^2$.
Prima di fare un esempio pratico, osserviamo che devono essere soddisfatte le seguenti condizioni sulle probabilità teoriche e sulle frequenze osservate e teoriche: $$\begin{array}{l}\sum\limits_{i=1}^k\hat{p}_i=1\\ \sum\limits_{i=1}^kn_i=\sum\limits_{i=1}^k\hat{n}_i=n\end{array}$$
Esempio
Due anni fa il responsabile di un supermercato, con riferimento ad un certo prodotto, ha rilevato che le marche A e C erano ugualmente preferite, che il 33% preferiva la marca B e il 27% la marca D. Una recente indagine su un campione casuale di clienti ha prodotto i seguenti risultati: A=44, B=70, C=28, D=50. C'è stata una variazione nelle preferenze dei consumatori?
Le ipotesi da sottoporre a verifica sono: $$\begin{cases} H_0: & \mbox{Non c'è stata variazione nelle preferenze dei consumatori}\\ H_1: & \mbox{C'è stata variazione nelle preferenze dei consumatori}\end{cases}$$
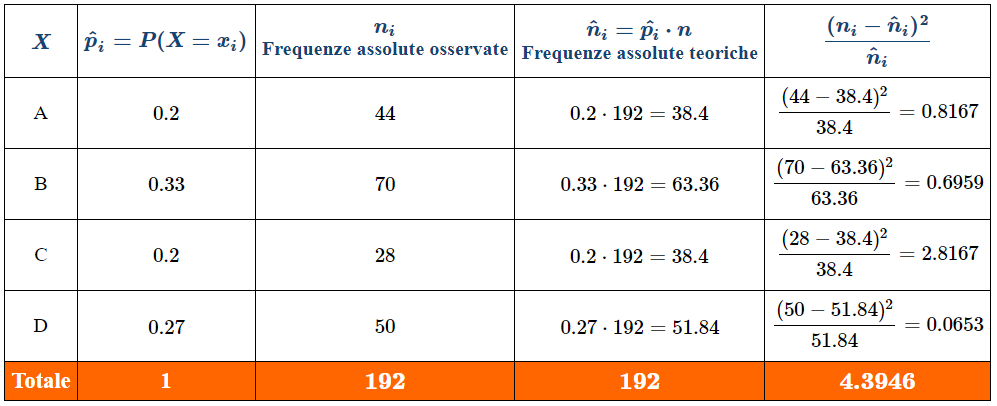
La tabella seguente riassume tutti i passaggi necessari per il calcolo della statistica $\chi^2$.
Inoltre, essendo $k-1=4-1=3$ i gradi di libertà e scegliendo $\alpha=0.05$ come livello di significatività del test, il valore critico letto dalle tavole della distribuzione chi-quadro è: $$\chi^2_{3,0.05}=7.81$$
Dato che $\chi=4.3946 < \chi^2_{3,0.05}=7.81$, si conclude dicendo che non ci sono prove sufficienti per rifiutare $H_0$ e che quindi non c'è stata variazione nelle preferenze dei consumatori.