Strettamente legata alla distribuzione della varianza campionaria, è la distribuzione del rapporto della varianze di due campioni indipendenti.
Tale distribuzione è necessaria per condurre un test di ipotesi sul rapporto tra due varianze, oppure in quei test di ipotesi in cui bisogna stabilire a priori se due campioni provengono da popolazioni aventi la stessa varianza, oppure ancora per un confronto tra due o più valori medi di gruppi di dati provenienti da un campione.
Poichè spesso non si conoscono le varianze delle due popolazioni, qualunque confronto viene fatto basandosi sulle varianze campionarie.
A tal proposito, supponiamo di avere due popolazioni normali con varianze rispettivamente $\sigma_1^2$ e $\sigma_2^2$ e due campioni da esse estratti aventi rispettivamente ampiezza $n_1$ e $n_2$; indicando con $S_1$ e $S_2$ le varianze campionarie, definiamo la variabile aleatoria $$\bbox[#ffffff,5px,border:2px solid #ff6600]{F=\frac{S_1^2/\sigma_1^2}{S_2^2/\sigma_2^2}}$$ avente distribuzione F o distribuzione di Fisher-Snedecor con $\nu_1=n_1-1$ gradi di libertà del numeratore e $\nu_2=n_2-1$ gradi di libertà del denominatore
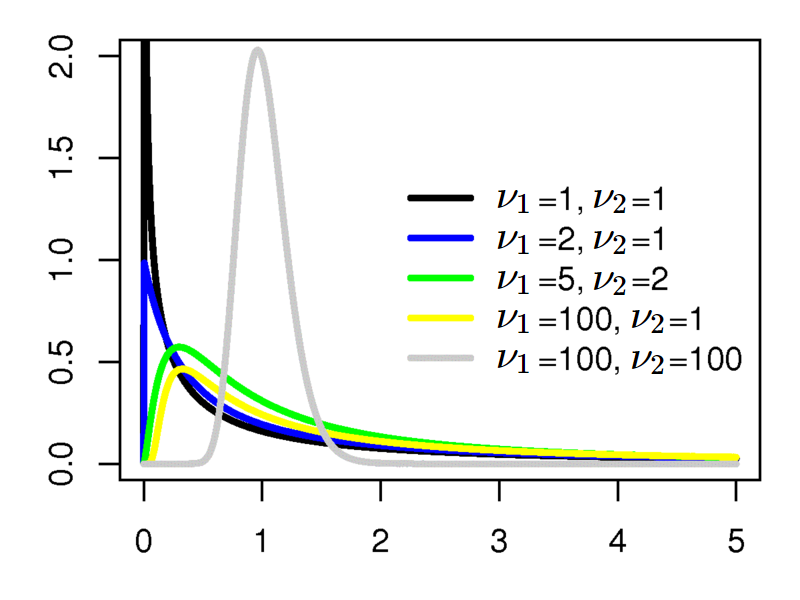
Di seguito la funzione di densità della F di Fisher al variare dei gradi di libertà.
Calcolo dei valori critici di F
Come per tutte le altre variabili aleatorie, anche per quella di Fisher disponiamo di tavole in cui sono tabulati i principali valori di $F$ assegnati i gradi di libertà $\nu_1$ e $\nu_2$ e il livello di significatività o errore di prima specie $\alpha$.
Qui puoi trovare alcuni valori scelti di $F_{\alpha}$ per varie combinazioni dei gradi di libertà $\nu_1$, $\nu_2$, dove $F_{\alpha}$ è tale che l'area sottesa dalla coda destra della distribuzione è pari ad $\alpha$ come si vede dalla figura qui in basso

Le tavole della distribuzione F di Fisher possono essere usate anche per calcolare l'area sinistra sottesa dalla curva mediante la seguente identità: $$F_{1-\alpha}(\nu_1,\nu_2)=\frac{1}{F_{\alpha}(\nu_2,\nu_1)}\quad (\large\star)$$
Esempio
Data la distribuzione F con gradi di libertà $\nu_1=15$ e $\nu_2=25$, trovare:
- $F_{0.10}(15,25)$
- $F_{0.90}(15,25)$
Consultando le tavole a pagina 4 del pdf leggiamo $$F_{0.10}(15,24)=1.78$$ e per la $(\large\star)$ otteniamo: $$F_{0.90}(15,25)=\frac{1}{F_{0.10}(24,15)}=\frac{1}{1.90}=0.5263$$



