I numeri relativi indicano tutti quei numeri che hanno il segno ($+$ o $-$) e il loro insieme viene indicato con $\mathbb{Z}$. La loro rappresentazione sulla retta dei numeri è la seguente:
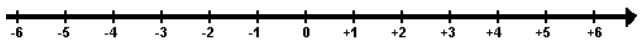
Per il confronto di due numeri relativi bisogna considerare la retta: è più grande il numero che sta dopo percorrendo la retta nel senso fissato.
Un numero relativo è formato dal segno e dal modulo o valore assoluto.
- Segno = $+$ e $-$
- Modulo o valore assoluto = numero senza segno
Esempio
- $+5 =$ numero relativo
- $+ =$ segno
- $+ =$ segno
Esempio
- $-5 =$ numero relativo
- $- =$ segno
- $5 =$ Modulo
Confronto di due numeri relativi
Due numeri relativi sono:
- Concordi, quando hanno lo stesso segno (Es: $+5$ e $+18$)
- Discordi, quando il segno è diverso (Es: $+5$ e $-18$)
- Uguali, quando hanno lo stesso segno e lo stesso modulo (Es: $+5$ e $+5$)
- Opposti, quando hanno lo stesso modulo e segno diverso (Es: $+5$ e $-5$)
- Se due numeri relativi sono positivi è più grande quello con il modulo più grande (Es: $+5 > +3$)
- Se due numeri relativi sono negativi è più grande quello con il modulo più piccolo (Es: $-5 > -7$)
$0$ è un numero neutro ed è maggiore di un numero negativo e minore di un numero positivo. Quindi $-n < 0 < +n$



