Una applicazione di moto uniformemente accelerato è la caduta libera di un corpo (in cui si trascurano gli effetti di attrito dovuti alla resistenza dell'aria), dove il valore dell'accelerazione (costante) è $a=9.8 m/s^2$. Il segno dell'accelerazione dipende da come fissiamo il sistema di riferimento iniziale. Per fissare le idee, consideriamo lo zero al suolo e fissiamo l'asse lungo cui si muove il corpo rivolto verso l'alto. Possiamo indicare questo asse, ad esempio, con $x$.
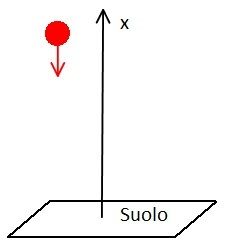
La caduta libera di un corpo da altezza $h$ ed inizialmente fermo ($x_0=h, v_0=0$) seguirà allora le leggi $$x(t)= x_0 + v_0 (t-t_0) + \frac{1}{2} a (t-t_0)^2$$ dove però l'accelerazione risulterà negativa per come abbiamo scelto il nostro sistema di riferimento (che ha direzione positiva dal basso verso l'alto).
Andiamo allora a sostituire $a=-g=-9.8 m/s^2, \quad x_0=h, \quad v_0=0, \quad t_0=0$. Otteniamo quindi:
$$x(t)= h- \frac{1}{2} gt^2$$
Con gli stessi accorgimenti l'espressione della velocità in funzione del tempo è:
$$v(t)= v_0 + a(t-t_0) = -gt$$
negativa come ci aspettavamo.
Cosa succede al suolo? In particolare, chiediamoci quale sia il tempo di caduta al suolo e la velocità della particella quando arriva a terra. Quello che bisogna fare, rispettivamente, è imporre che $x=0$ nell'espressione di $x(t)$ e ricavare la velocità per il valore di $t$.
$$0=h- \frac{1}{2} gt^2 \Longrightarrow t^2=\frac{2h}{g} \Longrightarrow t = \sqrt{\frac{2h}{g}}\quad \mbox{TEMPO DI CADUTA AL SUOLO}$$ $$ |v| = |-gt| = g \sqrt{\frac{2h}{g}} = \sqrt{2gh} \quad \mbox{VELOCITÀ AL SUOLO}$$
Consideriamo adesso il caso in cui la pallina venga lanciata al suolo con una velocità $v_1$. Dalla direzione dello spostamento capiamo che $v_1$ sarà una quantità negativa, $-v_1$, quindi la velocità iniziale del moto, sempre uniformemente accelerato con $a=-g$, sarà $v_0 = -v_1$. Le espressioni di posizione e velocità nel tempo diventano quindi:
$$x(t)= x_0 + v_0 (t-t_0) + \frac{1}{2} a (t-t_0)^2 = h - v_1 t -\frac{1}{2} g t^2 $$ $$v(t)= v_0 + a(t-t_0) = -v_1 - gt $$
Anche in questo caso possiamo calcolare il tempo di caduta al suolo e la velocità di arrivo a terra, utilizzando la stessa tecnica di prima ($x=0$):
$$gt^2+2v_1t-2h=0 \Longrightarrow t= \frac{-v_1 \pm \sqrt{v_1^2 + 2gh}}{g} \Longrightarrow t = \frac{-v_1}{g} + \sqrt{\frac{-v_1 ^2}{g^2} + \frac{2h}{g}}$$
dove abbiamo considerato solo la radice positiva trattandosi di una variabile temporale.
$$ v = -v_1 -g \left( -\frac{-v_1}{g} + \frac{\sqrt{v_1 ^2 + 2gh}}{g} \right) = -v_1 + v_1 -\sqrt{v_1 ^2 +2gh} = -\sqrt{v_1 ^2 +2gh}$$
Infine, supponiamo che la pallina venga lanciata verso l'alto (a partire dal suolo).
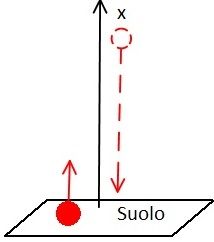
In questo caso, la pallina sale verso l'alto $x_0=0, \quad v_0 = v_2>0$. L'accelerazione, che in questo sistema è negativa, frena la pallina che ad un certo istante $t_c$ si ferma e torna indietro ricandendo verso il basso con velocità iniziale $v_0=0$ seguendo la dinamica dell'esempio di caduta libera. Quanto vale $t_c$ e dove si ferma la pallina $x_c$? Le equazioni della dinamica sono:
$$ x(t)= x_0+v_0(t-t_0)+\frac{1}{2} a(t-t_0)^2 = v_2t- \frac{1}{2} gt^2$$
e
$$v(t) = v_0 + a(t-t_0) = v_2 - gt $$
Quando la pallina si ferma in alto, la sua velocità è nulla $v(t)=0$ da cui ricaviamo che $$t = t_c = \frac{v_2}{g}$$ e $$x = x_c= v_2 t_c - \frac{1}{2} g t_c ^2 = \frac{v_2 ^2}{g} - \frac{1}{2} \frac{v_2^2}{g} = \frac{v_2^2}{2g}$$
Quando ricade la legge oraria sarà: $$ x(t)= h- \frac{1}{2} gt^2$$ dove $h = x_c = \frac{v_2^2}{2g}$ e $$v(t)= -gt$$. Il tempo di caduta al suolo è $$t = \sqrt{\frac{2h}{g}} = \sqrt{\frac{2}{g} \frac{v_2^2}{2g}} = \frac{v_2}{g} = t_c$$ cioè il tempo di caduta al suolo è uguale al tempo di risalita. Per concludere, il tempo complessivo del moto è quindi $2 t_c = 2\frac{v_2}{g}$.



