Moto rettilineo
Il moto rettilineo si svolge lungo una retta sul quale fissiamo ad arbitrio un'origine ed un verso. Basterà quindi una sola funzione, $x(t)$, per descrivere il moto di una particella. Pensiamo ad esempio, di voler descrivere il moto di una bicicletta che si muove il linea retta.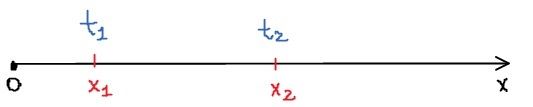
Fissato quindi il sistema di riferimento, indichiamo con $x_1$ e $x_2$ le posizioni in cui passa la bici agli istanti di tempo, $t_1$ e $t_2$ rispettivamente. Per descrivere il moto introduciamo una quantità che ne descriva il suo comportamento medio. In particolare, definiamo la velocità media $v_m$ come la rapidità con cui avviene lo spostamento dalla posizione $x_1$ alla posizione $x_2$ e che quindi sarà definita come il rapporto tra la variazione dello spazio e l'intervallo di tempo considerato:
$$v_m = \frac{x_2 - x_1}{t_2-t_1} = \frac{\Delta x}{\Delta t} $$
Essendo questa una quantità media, essa non fornisce informazioni sul comportamento effettivo della particella tra $x_1$ e $x_2$, piuttosto sul suo comportamento medio. Supponendo sempre $t_2 > t_1$, il segno della velocità media è determinato da $\Delta x$:
- se $x_2 > x_1$ la particella (bici) si muoverà nel verso positivo delle $x$ e quindi alla fine del moto la particella occuperà una posizione più "in avanti" rispetto a quella in cui è partita;
- se $x_2 < x_1$ la particella (bici) si muoverà nel verso negativo delle $x$ e quindi alla fine del moto la particella si troverà "più indietro" rispetto a dove è partita.
Per descrivere invece i dettagli del moto è più utile introdurre la velocità istantanea $v(t)$ che fornisca informazioni sulla rapidità di variazione della posizione per ogni istante di tempo $t$. Essa si ottiene come limite della velocità media quando l'intervallo di tempo va a zero:
$$v(t) = \lim_{\Delta t \rightarrow 0} \frac{\Delta x}{\Delta t} = \frac{dx}{dt}$$
dove l'ultima formula rappresenta la derivata della posizione rispetto al tempo.
Da quest'ultima definizione troviamo che $$dx = v(t) dt \Rightarrow \int_{x_0}^x d\tau = \int_{t_0}^t v(s) ds \Longleftrightarrow \Delta x = \int_{t_0}^t v(s) ds$$
Da questo ricaviamo che in un moto rettilineo lo spazio percorso è dato da:
$$x(t) = x_0 + \int_{t_0}^t v(s) ds$$
dove $x_0$ è la posizione iniziale della particella.
Applicando adesso la definizione di velocità media, troviamo una relazione che lega velocità media e velocità istantanea:
$$v_m = \frac{\Delta x}{\Delta t} = \frac{\int_{t_0}^t v(s) ds}{\Delta t} = \frac{1}{t-t_0} \int_{t_0}^t v(s) ds$$
dove $t_0$ è l'istante in cui inizia il moto.
La velocità nel tempo non è di solito una funzione costante, allora ha senso studiare la sua variazione nel tempo, ovvero l'accelerazione. Anche per l'accelerazione possiamo definire un valore medio ed uno istantaneo, definiti rispettivamente come:
$$ a_m = \frac{v_2 - v_1}{t_2-t_1} = \frac{\Delta v}{\Delta t} $$
dove $v_1$ e $v_2$ sono le velocità della particella negli istanti $t_1$ e $t_2$. In generale se l'accelerazione varia nel tempo il moto si dice accelerato.
$$ a(t) = \lim_{\Delta t \rightarrow 0} \frac{\Delta v}{\Delta t} = \frac{dv}{dt} = \frac{d^2x}{dt^2} $$
cioè l'accelerazione istantanea è la derivata della velocità rispetto al tempo o la derivata seconda della posizione rispetto al tempo. Adesso, come prima, se ricaviamo la variazione della velocità in funzione dell'accelerazione ed integriamo ambo i membri otteniamo:
$$dv= a(t) dt \Longrightarrow \int_{t_0}^t dv = \Delta v = \int_{t_0}^t a(\tau)d\tau \Longrightarrow v(t)= v_0 + \int_{t_0}^t a(\tau) d\tau$$
che permette di ricavare la velocità istantanea se è nota l'accelerazione.
Osservazioni
- se $v > 0$ il moto è positivo, cioè la coordinata $x$ cresce, viceversa se $v<0$ il moto è negativo e quindi la coordinata $x$ decresce;
- se $a>0$ la velocità cresce nel tempo, mentre per $a<0$ la velocità decresce;
- l'unità di misura della velocità nel SI è $\left[ \frac{m}{s}\right]$. Si ha che : $$1 \frac{km}{h} = \frac{10^3 m}{3600 s} = 0.278 \frac{m}{s}$$ $$1 \frac{m}{s} =3.6 \frac{km}{h}$$
- l'unità di misura dell'accelerazione nel SI è $\left[ \frac{m}{s^2}\right]$.
Moto rettilineo uniforme
Il moto rettilineo uniforme è un moto rettilineo caratterizzato dal fatto che la velocità è costante nel tempo, quindi non ci sarà differenza tra velocità media e velocità istantanea. Per provare quanto detto e per introdurre le equazioni del moto, basta applicare l'unica ipotesi fatta fin'ora, cioè $v$ costante alle equazioni che abbiamo trovato per il moto rettilineo. Quindi:
$$x(t) = x_0 + \int_{t_0}^t v(s) ds = x_0 + v \int_{t_0}^t ds = x_0 + v (t-t_0)$$
dove $x_0$ è la posizione all'istante di tempo iniziale $t_0$.
$$v_m = \frac{1}{t-t_0} \int_{t_0}^t v(s) ds = v (t-t_0) \frac{1}{t-t_0}$$
Essendo infine l'accelerazione la derivata della velocità, essa risulterà chiaramente nulla in quanto derivata rispetto al tempo di una funzione costante in $t$
$$a(t) = \frac{dv}{dt} =0$$
I grafici della posizione rispetto al tempo saranno delle rette, in quanto $x(t)$ è lineare in $t$, mentre quelli della velocità saranno segmenti o rette parallele all'asse delle ascisse.

Moto rettilineo uniformemente accelerato
Il moto rettilineo uniforme è un moto rettilineo caratterizzato dal fatto che l'accelerazione è costante nel tempo. Per introdurre le equazioni del moto, basta applicare l'unica ipotesi fatta fin'ora, cioè $a$ costante alle equazioni che abbiamo trovato per il moto rettilineo. Quindi:
$$v(t)= v_0 + \int_{t_0}^t a(\tau) d\tau = v_0 + a(t-t_0)$$
cioè la velocità è una funzione lineare nel tempo
$$x(t) = x_0 + \int_{t_0}^t v(s) ds = x_0 + \int_{t_0}^t [v_0 + a (\tau-t_0)] d\tau = x_0 + v_0 (t-t_0) + \frac{1}{2} a (t-t_0)^2$$
cioè lo spazio è una funzione quadratica nel tempo. Quindi i grafici della posizione rispetto al tempo saranno archi di parabole, quelli della velocità rette e quelli dell'accelerazione segmenti o rette parallele all'asse delle ascisse.




