Cos'è un vettore? Pensate di essere a Tortona (un paesino tra Milano e Genova) e di dover andare a Milano per lavoro. Decidete di prendere l'autostrada A7, che collega Genova e Milano. Allora dovrete: imboccare l'A7 (cioè scegliere la direzione "autostrada"), immettervi nella giusta corsia (cioè scegliere se andare verso Milano o verso Genova) e percorrere circa 80 km. Supponendo di poter approssimare l'autostrada con un segmento, avremo dato al nostro viaggio una direzione (A7), un verso (Genova-Milano) ed un modulo (80 km). Non abbiamo fatto altro che descrivere il nostro spostamento con un vettore. In fisica, in generale, un vettore non indicherà solo uno spostamento, ma qualsiasi entità fisica che potrà essere descritta con un modulo, una direzione ed un verso: pensate alla velocità, all'accelerazione, alle forze (per andare a "Le forze come vettori" clicca qui), al campo elettrico e magnetico e così via. Per rappresentare un vettore si utilizzerà dunque una freccia e lo si indicherà con una piccola freccia sul nome del vettore $\vec{a}$.

Le quantità che invece possono essere descritte solo da un numero, saranno dette scalari: basta pensare alla massa, al tempo, alla lunghezza e così via.
Molto spesso è utile saper sommare e sottrarre i vettori per capire appunto il vettore risultante dall'interazione di uno o più vettori (ad esempio se un corpo è soggetto a due forze e quindi a due vettori diversi, sarà interessante capire a quale forza totale sarà soggetto il corpo).
Regola della somma di vettori (metodo punta-coda)
Dati due vettori $\vec{a}$ e $\vec{b}$, se $\vec{b}$ è applicato al punto terminale di $\vec{a}$, per trovare graficamente il vettore somma $\vec{c} = \vec{a}+\vec{b}$, basta unire l'origine di $\vec{a}$ con l'estremità finale di $\vec{b}$.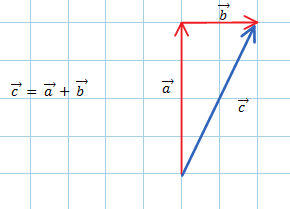
Regola del parallelogramma
Dati due vettori $\vec{a}$ e $\vec{b}$, se $\vec{b}$ è applicato al punto terminale di $\vec{a}$, per trovare graficamente il vettore somma $\vec{c} = \vec{a}+\vec{b}$, basta spostare in modo parallelo a se stesso il vettore $\vec{b}$ fino al punto iniziale del vettore $\vec{a}$ e considerare come vettore somma la diagonale del parallelogramma che ha come lati i due vettori $\vec{a}$ e $\vec{b}$.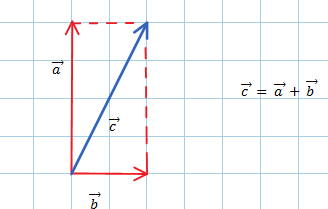
La proprità di somma gode della proprità commutativa: $\vec{a} + \vec{b} = \vec{b} + \vec{a}$.
In entrambi i casi per calcolare il modulo del vettore somma basterà applicare la formula $$|\vec{c}| = \sqrt{\left|\vec{a}\right|^2 + \left|\vec{b}\right|^2}$$ dove con il simbolo $|\vec{c}|$ indichiamo il modulo del vettore $\vec{c}$ e così via.
Ad esempio se il modulo del vettore $|\vec{a}| = 3 m$ e il modulo del vettore $\vec{b}=4 m$, allora il modulo del vettore somma che indichiamo con $\vec{c} = \vec{a} + \vec{b} = \sqrt{3^2 + 4^2} = \sqrt{9+16} = \sqrt{25} = 5 m$.
Da quanto esposto sopra è chiaro che la somma di vettori sarà ancora un vettore con un suo modulo, direzione e verso. Gli ultimi due si riescono a determinare da un punto di vista grafico mentre il modulo lo si può trovare analiticamente con la formula della radice quadrata appena vista.
Prodotto di vettori per uno scalare (numero)
Dato un vettore $\vec{a}$ e un numero reale $m$, si definisce il prodotto $m \vec{a}$ di un numero reale per un vettore $\vec{a}$ il vettore che ha per direzione la stessa direzione del vettore $\vec{a}$, lo stesso verso del vettore $\vec{a}$ se il numero $m$ è positivo, altrimenti verso opposto se $m$ è negativo e modulo pari al prodotto del modulo del vettore $\vec{a}$ per $m$: cioè $|m \vec{a}| = m |\vec{a}|$.Regola della differenza tra vettori
Dati due vettori $\vec{a}$ e $\vec{b}$, poichè $\vec{a} - \vec{b} = \vec{a} + (-\vec{b}) $, per rappresentare graficamente la differenza tra vettori basta applicare le regole della somma appena viste ai due vettori di partenza, di cui il sottraendo si considererà con verso opposto.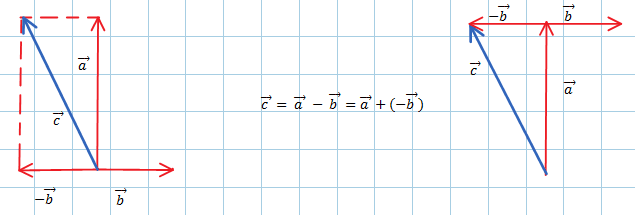
Si vede così che la differenza tra vettori coincide con l'altra diagonale del parallelogramma utilizzato per il calcolo del vettore somma.



