Abbiamo visto come si formula una legge fisica utilizzando il metodo sperimentale. Adesso vediamo come rappresentare una legge, in particolare, utilizzando un punto di vista grafico.
Se abbiamo due grandezze fisiche legate tra loro, infatti, possiamo eseguire una rappresentazione della relazione che le lega su un sistema cartesiano nel piano. Avere una relazione tra grandezze vuol dire che riusciamo a determinare il valore di una delle due, noto l'altro. Chiameremo spesso le due grandezze in gioco con i simboli $x$ e $y$.
Viceversa se misuriamo in modo sperimentale i valori di due grandezze fisiche tra loro dipendenti, possiamo riportare questi valori uno sull'asse delle ascisse e l'altro su quello delle ordinate e individuare così un punto sul piano, chiamiamolo ad esempio A, che ha come coordinate i valori misurati.
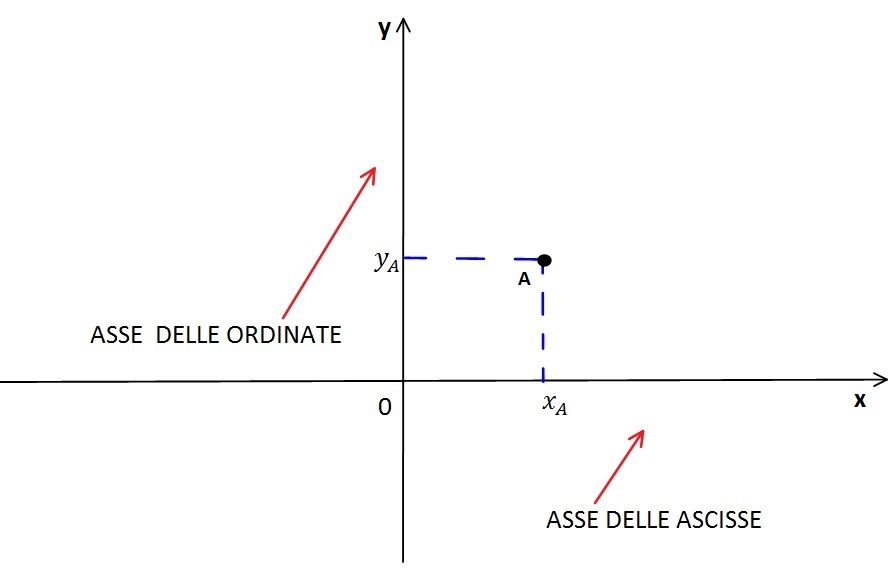
In questo modo ad ogni misura delle due grandezze corrisponde un punto del piano e congiungendo tutti i punti che rappresentano le grandezze si può risalire alla legge matematica che lega le due grandezze.
La proporzionalità diretta (caso lineare)
Consideriamo due grandezze che chiameremo sempre $x$ e $y$. Se una delle due grandezze, ad esempio $y$ varia al variare di $x$ in modo tale che se $x$ raddoppia, triplica, ecc.. anche $y$ raddoppia, triplica, ecc... allora si dice che $y$ è espressa in funzione di $x$ da una legge di proporzionalità diretta. Tale legge ha sempre la forma
$$ y = k x $$
dove $k$ è la costante (cioè un numero) che rappresenta il rapporto tra le due grandezze, chiamata costante di proporzionalità. La legge $y = kx$ si rapprensenta nel piano cartesiano come una retta che passa per l'origine.
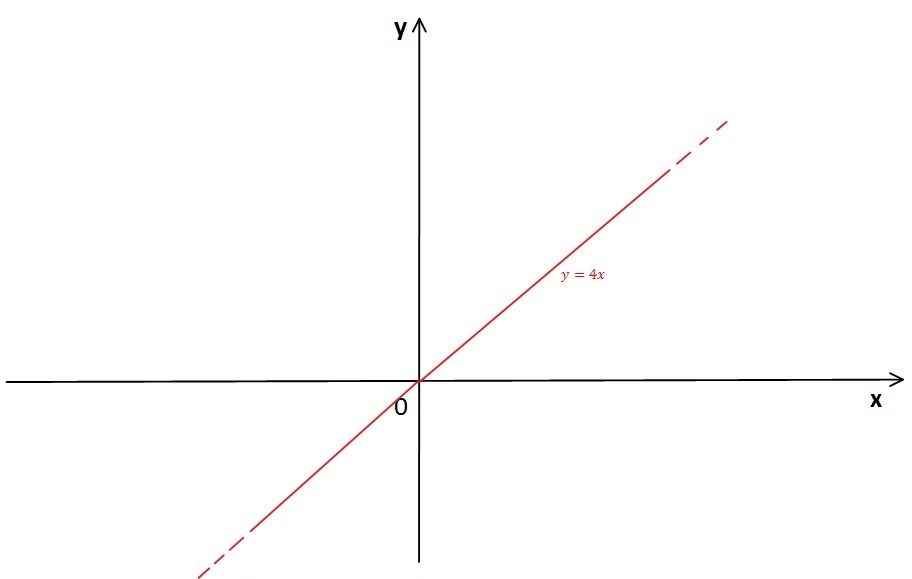
Quindi se abbiamo dei dati sperimentali, che rappresentati graficamente danno luogo ad una retta, possiamo sicuramente affermare che le due grandezze che abbiamo misurato sono legate da proporzionalità diretta. Viceversa, se conosciamo la legge che lega due grandezze e ci accorgiamo che essa è di tipo lineare e quindi che le due grandezze sono legate da proporzionalità diretta, possiamo risalire ai valori di una grandezza, nota l'altra.
Supponiamo quindi di aver misurato sperimentalmente la massa e il volume di un pezzo di alcuni pezzi di ferro e di schematizzarli nella seguente tabella: quando il volume del corpo è $ 1 m^3 $ (metro cubo), la sua massa è $ 8 kg $; quando il volume del corpo è $2 m^3 $, la sua massa è $ 16 kg$; quando il volume del corpo è $ 3 m^3 $, la sua massa è $ 24 kg$ e così via.

Dalla tabella si osserva che se il volume raddoppia (quindi dal valore 1 passiamo al valore 2) anche la massa raddoppia (passiamo dal valore 8 al valore 16), il volume triplica (quindi dal valore 1 passiamo al valore 3) anche la massa triplica (passiamo dal valore 8 al valore 24), e così via... Le due grandezze, volume e massa, sono quindi legate da proporzionalità diretta: possiamo quindi scrivere:
$$ M = 8 V $$
visto che la costante di proporzionalità che rappresenta il valore del rapporto tra le due grandezze è proprio $8$.
(Osserva che $\frac{8}{1} = 8, \quad \frac{16}{2}=8, \quad \frac{24}{3} = 8 \quad \dots \quad \frac{40}{5}= 8 = k $ ).
Se rappresentiamo quindi sull'asse delle ascisse il volume e sull'asse delle ordinate la massa, individuando così i punti di coordinate $(1, 8), (2, 16), (3,24), (4, 32), (5,40)$ ci rendiamo subito conto che la loro rappresentazione è una retta, in particolare la retta di equazione $M = 8V$ o usando $x$ e $y$ per indicare rispettivamente il volume e la massa $y = 8x$.
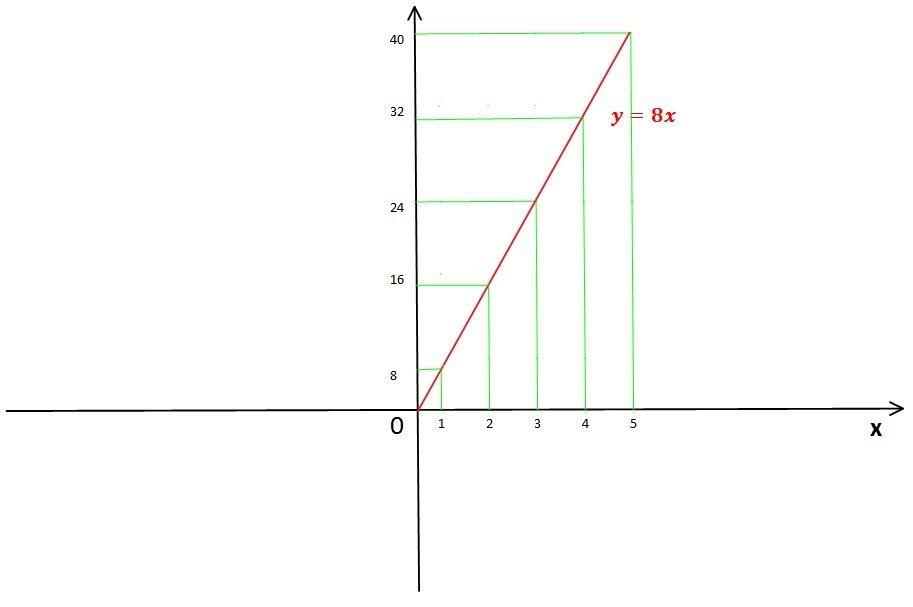
Vicerversa, se sappiamo che due grandezze $x$ e $y$ sono legate da una relazione del tipo $y = kx$, ad esempio $y = 8 x$, capiamo insieme che metodo utilizzare per rappresentare tale legge sul piano cartesiano. Si tratta di trovare due punti sul piano attraverso i quali passa la retta. Sicuramente la retta passerà per l'origine degli assi (infatti quando $x=0$, $y = 8 * 0 =0$). A questo punto scegliamo un altro valore da attribuire alla $x$, ad esempio $x=2$ ottenendo il valore di $y= 8*2=16$. Individuiamo così sul piano i punti di coordinate $(0,0)$ e $(2, 16)$ e congiugiamoli con una linea. La linea è la retta cercata.

Basta individuare solo due punti perchè per due punti passa una e una sola retta.
Infine espliciatiamo il fatto che, nota la legge (nel nostro caso $y = 8x$), se conosciamo il valore di una grandezza (ad esempio $x$) possiamo subito ricavare la seconda, cioè $y$ e che se le due grandezze sono legate da proporzionalità diretta, all'aumentare dell'una, aumenta anche l'altra.
Proporzionalità inversa
Consideriamo, ora, tutti i rettangoli che hanno per area un valore assegnato e chiamiamo tale valore $A$. Ricordiamo che in un rettangolo l'area è data dal prodotto dei lati. Chiamiamo allora $x$ e $y$ i lati del rettangolo. Per quanto detto si ha $$ xy=A$$ ovvero $$y = \frac{A}{x}$$
In questo caso si dice che un lato del rettangolo è inversamente proporzionale alla misura dell'altro lato o che la legge appena scritta rappresenta una legge di proporzionalità inversa tra le grandezze $x$ e $y$. Si osserva dalla legge che all'aumentare di $x$, la $y$ diminuisce. Eseguendo gli stessi passaggi logici del paragrafo precedente, troviamo che la curva che si ottiene dalla rappresentazione della legge di proporzionalità inversa è una iperbole equilatera, ovvero una curva di questo tipo




