Seconda legge di Newton
La somma di tutte le forze agenti su un corpo di massa $m$ e di accelerazione $\vec{a}$ è dato dal prodotto di massa e accelerazione: $$\sum \vec{F} = m \vec{a} $$Cioè, quando su un oggetto di massa $m$ agisce una forza risultante $\sum \vec{F}$, l'oggetto subisce un'accelerazione $\vec{a}$ che:
- è direttamente proporzionale alla forza risultante
- è inversamente proporzionale alla massa
- ha direzione e verso uguali e concordi a quelli della forza
$$\bbox[#ffffff,5px,border:2px solid #ff6600] {\vec{a} = \frac{\sum \vec{F}}{m} \quad\mbox{ovvero}\quad \sum \vec{F} = m\cdot \vec{a}}$$
Nel SI l'unità di misura delle forze è il Newton il cui simbolo è $N$.Sarà necessaria una forza di un Newton per imprimere un'accelerazione di $1 m/s^2$ a una massa di $1 Kg$, cioè $$1 N = (1 Kg)\cdot(1 m/s^2)$$Il Newton è, quindi, un'unità di misura derivata.
Inoltre, osserviamo che poichè forze e accelerazioni sono vettori, l'equazione del secondo principio della dinamica è un'equazione vettoriale. Per questo, nei problemi in due dimensioni, conviene scomporre i vettori nelle loro componenti cartesiane e considerare il secondo principio della dinamica nelle due equazioni$$\sum \vec{F_x} = m \vec{a}_x$$ $$\sum \vec{F_y} = m \vec{a}_y$$
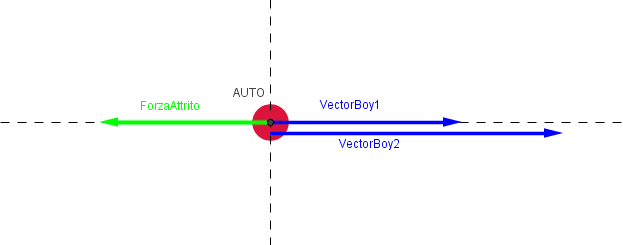
Per risolvere problemi di cui si cerca di calcolare la forza risultante di un oggetto applicando la seconda legge della dinamica è conveniente schematizzare tutte le forze in gioco mediante un diagramma di corpo libero, cioè uno schema in cui si rappresentino tutte le forze (come vettori) agenti sul corpo.
Ad esempio, se volessimo fare il diagramma delle forze di un'automobile guasta spinta da due ragazzi, dovremo rappresentare le due forze impresse dai ragazzi (quindi concordi e verso destra) e la forza di attrito che agisce sull'automobile che si oppone in verso alla risultante delle forze applicate dai due ragazzi.