Campo elettrico all'interno e all'esterno di una superficie sferica carica
Prendiamo in considerazione una sfera di raggio R con carica superficiale q e densità di carica $\sigma$ e calcoliamo il campo elettrico nei dintorni di tale superficie.
Campo elettrico all'esterno della sfera
In un punto P distante r > R dal centro della sfera il campo elettrico E è certamente radiale, in quanto, essendo la carica distribuita uniformemente su tutta la superficie, esso sarà dato dalla somma di vettori simmetrici a due a due e con uguale modulo. Questo vuol dire che l'intensità del campo elettrico è uguale in tutti i punti P equidistanti r dal centro della sfera ed è in direzione ortogonale rispetto alla superficie (con verso uscente se la carica è positiva, con verso entrante se è negativa).
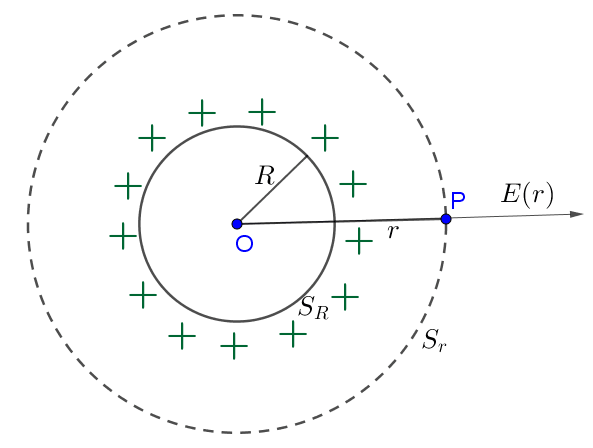
Il flusso del campo elettrico nel punto P è: $$\Phi (E)=\int_{S_r}\vec{E}(r)\cdot d\vec{S}_r=E(r)\int_{S_r} d\vec{S}_r=E(r)\cdot 4\pi r^2$$ dove $S_r$ è la superficie sferica di raggio r concentrica a quella data, $E(r)$ è il campo elettrico nel punto P che dipende solo da r.
Per il teorema di Gauss: $$\Phi (E)=\frac{Q_{int}}{\varepsilon_0}=\frac{q}{\varepsilon_0}$$ e per definizione di densità superficiale $$\sigma=\frac{Q}{S_R}=\frac{q}{4\pi R^2}$$ abbiamo che $$E(r)\cdot 4\pi r^2=\frac{q}{\varepsilon_0}$$ e quindi $$E(r)=\frac{q}{4\pi\varepsilon_0 r^2}=\frac{\sigma R^2}{\varepsilon_0 r^2}$$
Campo elettrico all'interno della sfera
All'interno della superficie sferica valgono le stesse ragioni di simmetria e quindi anche in questo caso il campo è radiale. Ma poichè dentro la sfera non c'è carica, il flusso attraverso qualsiasi superficie sferica interna a $S_R$ è nullo, per il teorema di Gauss anche il campo elettrico è nullo.



