Sia $f(x):D\longrightarrow\mathbb{R}$ una funzione e $x_0\in D$. $x_0$ si dice punto di non derivabilità
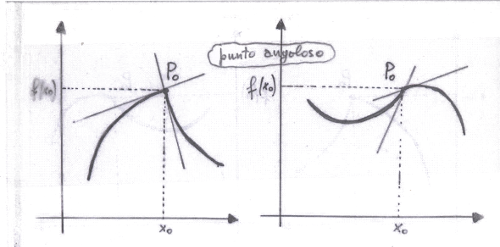
- angoloso se esistono finite derivata destra e sinistra in $x_0$ ma sono diverse: $$\begin{array}{c} f'_-(x_0)=\lim\limits_{h\rightarrow 0^-}\frac{f(x_0+h)-f(x_0)}{h}=L_1\in\mathbb{R}\\ \neq\\ f'_+(x_0)=\lim\limits_{h\rightarrow 0^+}\frac{f(x_0+h)-f(x_0)}{h}=L_2\in\mathbb{R}\end{array}$$
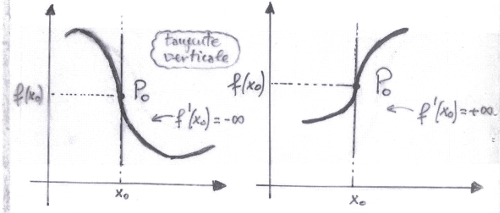
- a tangente verticale se $f$ è continua in $x_0$ e $f'(x_0)=\pm\infty$
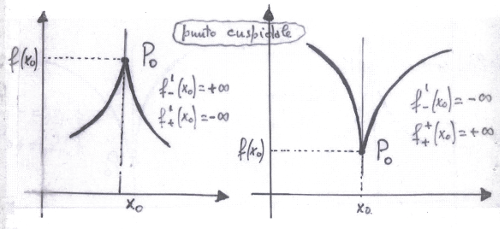
- cuspidale se $f$ è continua in $x_0$ e $$f'_-(x_0)=-\infty\quad\mbox{e }f'_+(x_0)=+\infty$$ oppure $$f'_-(x_0)=+\infty\quad\mbox{e }f'_+(x_0)=-\infty$$