Sia $f:(a,b)\rightarrow\mathbb R$ una funzione e sia $x_0\in (a,b)$. Si dice che $x_0$ è un punto di:
- MASSIMO RELATIVO per $f\quad\Leftrightarrow\quad\exists\ I(x_0)\subseteq (a,b):\ f(x)\le f(x_0) \forall x\in I(x_0)$
- MINIMO RELATIVO per $f\quad\Leftrightarrow\quad\exists\ I(x_0)\subseteq (a,b):\ f(x)\ge f(x_0) \forall x\in I(x_0)$
Nel seguente grafico di funzione, in punti $M_1$ ed $M_2$ sono massimi relativi e i punti $m_1$ ed $m_2$ sono minimi relativi.

Sia $f:(a,b)\rightarrow\mathbb R$ una funzione e sia $x_0\in (a,b)$. Si dice che $x_0$ è un punto di:
- MASSIMO ASSOLUTO per $f\quad\Leftrightarrow\quad f(x)\le f(x_0)\ \forall x\in (a,b)$
- MINIMO ASSOLUTO per $f\quad\Leftrightarrow\quad f(x)\ge f(x_0)\ \forall x\in (a,b)$
In particolare si dice che $x_0$ è massimo o minimo assoluto interno se è un punto interno ad $(a,b)$; si dice che $x_0$ è massimo o minimo assoluto di frontiera se è un punto di frontiera ($x_0=a$ oppure $x_0=b$).
Osservazione sugli estremi assoluti
I massimi e minimi assoluti sono anche massimi e minimi relativi
In figura, il punto $M_1$ è sia un massimo assoluto interno che massimo relativo. Non c'è nessun minimo assoluto o relativo ed inoltre non ci sono minimi o massimi di frontiera.

Teorema di Fermat (C.N. affinchè una $f$ presenti un max o un min relativo)
Sia $f:(a,b)\rightarrow\mathbb R$ una funzione e sia $x_0\in (a,b)$. Se $\exists\ f'(x_0)$ e $x_0$ è un punto di max o min relativo si ha:
$$f'(x_0)=0$$
Interpretazione geometrica del teorema di Fermat
Poichè la derivata prima calcolata in un punto rappresenta il coefficiente angolare della retta tangente nel punto stesso, il teorema di Fermat afferma che, in corrispondenza dei punti di minimo o di massimo relativo, la retta tangente è una retta orizzontale (infatti $m=f'(x_0)=0$) 
Osservazione sui punti con derivata nulla
La condizione $f'(x_0)=0$ è una condizione necessaria ma non sufficiente. Infatti, come vedremo di seguito, può capitare che una funzione abbia derivata prima nulla in un punto senza che, tale punto, sia un massimo o un minimo relativo.
Punti critici
I punti $x_0$ in cui la derivata prima si annulla (cioè $f'(x_0)$), sono detti punti critici
Classificazione dei punti critici
I punti critici possono essere dei seguenti tipi:
- punti di minimo o di massimo relativo per $f$;
Ad esempio, la funzione $f(x)=x^2+1$ ha un punto critico in $0$ poichè $f'(0)=0$ ed esso è pure un punto di minimo relativo (e assoluto).
Anche la funzione $f(x)=-x^2+2x$ ha un punto critico in $0$ ma stavolta esso rappresenta un punto di massimo relativo (e assoluto).

- punti in cui la $f$ è crescente o descrescente;
La funzione $f(x)=x^3$ ha banalmente un punto critico in $0$ e, in tale punto la funzione è crescente poichè:
- $f(x)=x^3 < 0=f(0)\quad$ in un intorno sinistro
- $f(x)=x^3 > 0=f(0)\quad$ in un intorno destro
Analogamente per la funzione $f(x)=-x^3$ che presenta un punto critico in $0$ in cui la $f$ è decrescente.

- punti diversi da 1) e 2).
Questo è il caso di una funzione la cui derivata si annulla in un punto $x_0$ senza presentare né un minimo né un massimo assoluto in $x_0$ e senza essere crescente o decrescente in $x_0$.
Ad esempio:
- $$f(x)=\begin{cases} x^2\cdot\cos\frac{1}{x}&\mbox{se } x\neq 0\\ 0&\mbox{se } x=0\end{cases}$$
ha derivata prima nulla in $x_0=0$ ed inoltre, in un qualunque intorno di $0$ la funzione non è né crescente e né decrescente come si può vedere dal grafico qui in basso.

C.S. per l'esistenza di min o max relativi per $f$
Teorema 1
Sia $f:(a,b)\rightarrow\mathbb R$ una funzione continua in $x_0$ punto interno ad $(a,b)$ tale che $\exists\ f'(x)\forall x \in I(x_0)$. Si ha:
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{\left.\begin{array}{r} f'(x)> 0\quad \forall x \in I_-(x_0)\\ f'(x) < 0\quad \forall x \in I_+(x_0)\end{array}\right\}\Rightarrow\quad x_0 \mbox{ max relativo per $f$}}$$ e $$\bbox[#ffffff,5px,border:2px solid #ff6600]{\left.\begin{array}{r} f'(x)< 0\quad \forall x \in I_-(x_0)\\ f'(x) > 0\quad \forall x \in I_+(x_0)\end{array}\right\}\Rightarrow\quad x_0 \mbox{ min relativo per $f$}}$$
Osservazione sull'importanza dell'ipotesi di continuità nel teorema 1
Il teorema appena enunciato non vale nel caso in cui la $f$ non sia continua in $x_0$. Basta, infatti osservare il seguente grafico:
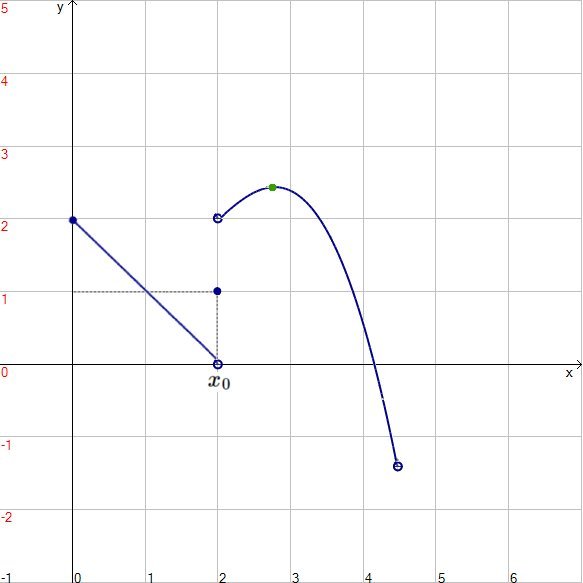
In un intorno sinistro del punto $x_0$ si ha che $f'(x)<0$, mentre in un intorno destro si ha che $f'(x)>0$. Però, poichè nel punto $x_0$ la funzione non è continua, tale punto NON è un massimo relativo.
Osserviamo, inoltre, che il teorema 1 rappresenta solo una condizione sufficiente ma non necessaria. A prova di ciò forniamo un controesempio che mostra che il viceversa di tale teorema non vale.
Controesempio sul viceversa del teorema 1
Consideriamo la seguente funzione definita in tutto $\mathbb R$
$$f(x)=x^2|x|=\begin{cases} x^3&\mbox{se } x\ge 0\\ -x^3&\mbox{se } x < 0\end{cases}$$Si ha che $x_0=0$ è un punto di minimo relativo, $f'(0)=f''(0)=0$ ma non esiste $f'''(0)$, infatti:
$$f'(x)=\begin{cases} 3x^2&\mbox{se } x\ge 0\\ -3x^2&\mbox{se } x < 0\end{cases},\quad f''(x)=\begin{cases} 6x&\mbox{se } x\ge 0\\ -6x&\mbox{se } x < 0\end{cases},\quad f'''(x)=\begin{cases} 6&\mbox{se } x\ge 0\\ -6&\mbox{se } x < 0\end{cases}$$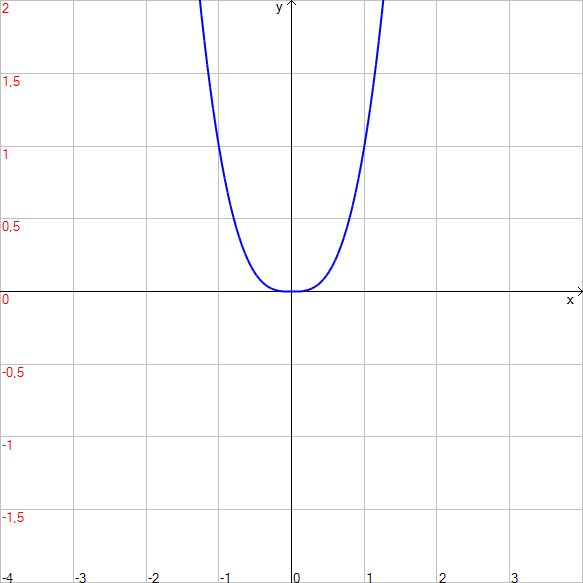
Teorema 2
Sia $f:(a,b)\rightarrow\mathbb R$ derivabile $n$ volte e sia $x_0\in (a,b)$ tale che $f'(x_0)=f''(x_0)=\dots=f^{(n-1)}(x_0)=0$ e $f^{(n)}(x_0)\neq 0$, allora:
- se $n$ pari e $f^{(n)}(x_0)<0\quad\Rightarrow\quad x_0$ max relativo
- se $n$ pari e $f^{(n)}(x_0)>0\quad\Rightarrow\quad x_0$ min relativo
- se $n$ dispari e $f^{(n)}(x_0)>0\quad\Rightarrow\quad f$ crescente in $x_0$
- se $n$ dispari e $f^{(n)}(x_0)<0\quad\Rightarrow\quad f$ decrescente in $x_0$
Analogamente a quanto fatto per il teorema 1 forniamo un controesempio che mostra che il viceversa di del teorema 2 non vale.
Controesempio sul viceversa del teorema 2
Consideriamo la seguente funzione definita in tutto $\mathbb R$
$$f(x)=\begin{cases} |x|&\mbox{se } x\neq 0\\ 1&\mbox{se } x = 0\end{cases}$$Si ha che $x_0=0$ è un punto di massimo relativo, ma la funzione presenta un punto di discontinuità di 3º specie in $0$, infatti:
$$\lim\limits_{\rightarrow 0}f(x)=\lim\limits_{\rightarrow 0}|x|=0\neq f(0)=1$$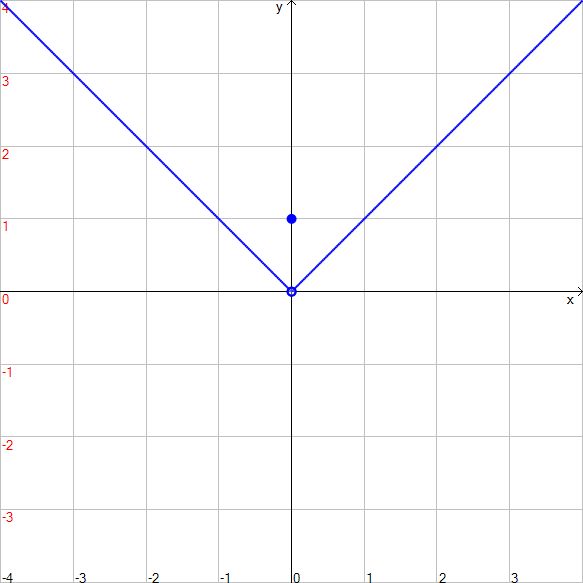
Breve schema per la ricerca degli estremi di una funzione
Per ricercare gli eventuali minimi e massimi relativi di una funzione bisogna seguire quanto segue:
- Se $f:(a,b)\rightarrow\mathbb R$ è derivabile in $(a,b)$ si trovano i punti critici risolvendo $f'(x)=0$ e si applicano il teorema 1 o il teorema 2 per decidere se sono punti di minimo o di massimo.
- Se $f$ non è derivabile in tutto $(a,b)$ occorre ricercare i punti critici distinguendone la loro natura come in 1) e verificare, tramite definizione, se i punti in cui non esiste la derivata prima sono punti di minimo o di massimo relativo.
Per ricercare gli eventuali minimi e massimi assoluti di una funzione bisogna confrontare i valori che la $f$ assume nei seguenti punti:
- punti critici, ($x\in (a,b):f'(x)=0$)
- punti in cui la $f$ non è derivabile ($x\in (a,b):\not\exists f'(x)$)
- punti di frontiera
Fatto ciò, il massimo assoluto (se esiste) sarà quella $x$ per la quale la funzione assume il valore più grande; mentre il minimo assoluto (se esiste) sarà quella $x$ per la quale la funzione assume il valore più piccolo.



