Sia dato un sistema lineare di $m$ equazioni in $n$ incognite $A\overline{x}=\overline{b}$ con $B$ matrice completa associata. Tale sistema è possibile se e soltanto se il rango della matrice completa $A$ coincide con il rango della matrice incompleta $B$:
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{A\overline{x}=\overline{b}\ \mbox{ possibile }\Leftrightarrow\ r(A)=r(B)}$$
In particolare, se $r(A)=r(B)=r$, si hanno 2 casi:
- $r=n$: sistema determinato;
- $r < n$: sistema indeterminato con $\infty^{n-r}$ soluzioni (dove $n-r$ rappresentano i gradi di libertà del sistema).
Se il sistema è possibile (determinato o indeterminato), gli step da seguire per il calcolo delle soluzioni sono i seguenti:
- Estrazione da $A$ di un minore di ordine $r$ a determinante non nullo.
- Riscrittura del sistema formato solo dalle $r$ equazioni corrispondenti alle righe del minore estratto.
- Se $r=n$, calcolo dell'unica soluzione del sistema tramite la regola di Cramer; se $r < n$, determinazione del valore delle $r$ incognite presenti nel minore, in funzione delle $n-r$ incognite rimanenti (i gradi di libertà).
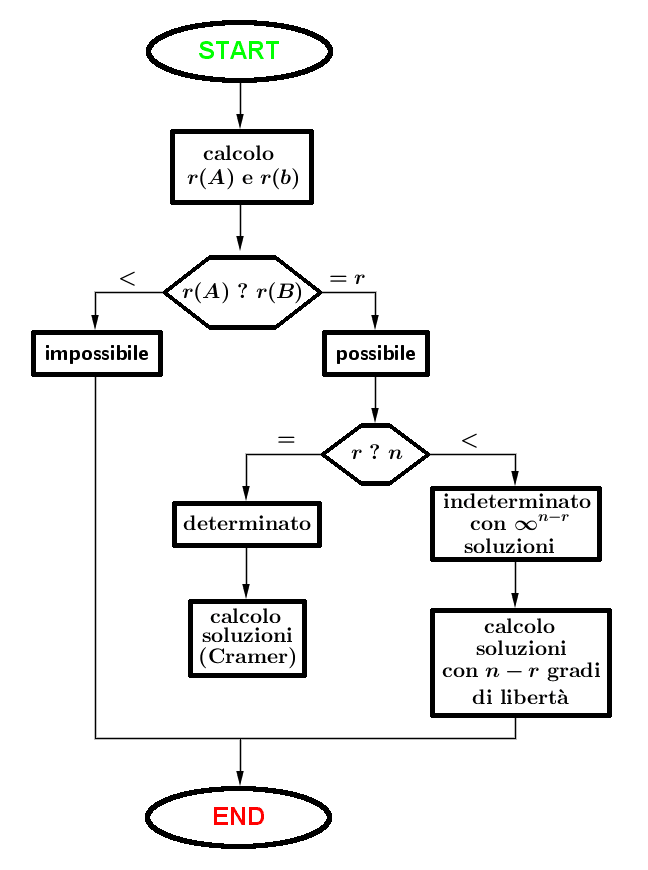
Di seguito lo schema a blocchi che riassume la procedura da seguire per la risoluzione di un qualunque sistema lineare $m\times n$.
Esempio di risoluzione di un sistema lineare tramite Rouchè-Capelli
Calcoliamo le soluzioni del seguente sistema
$$\begin{cases} x-y+2z=1\\ 2x+z=0\\ 2y-3z=-2\end{cases}$$In questo caso Cramer non ci fornisce molte informazioni dato che:
$$|A|=\left|\begin{matrix} 1 & -1 & 2\\ 2 & 0 & 1\\ 0 & 2 & -3\end{matrix}\right|=0$$(La 2° riga meno 2 volte la 1° riga equivale alla 3° riga. Per la proprietà 7 sui determinanti $|A|=0$). Il sistema è non determinato (cioè impossibile o indeterminato).
Applichiamo il teorema di Rouché capelli per capire se il sistema è possibile indeterminato o impossibile calcolando i ranghi della matrice incompleta e completa. Si vede che $r(A)=2$ considerando il minore a determinante non nullo che si ottiene estraendo gli elementi della 1° e 2° riga, 1° e 2° colonna
$$M=\left(\begin{matrix} 1 & -1\\ 2 & 0\end{matrix}\right)$$Passiamo a $B$:
$$B=\left(\begin{matrix} 1 & -1 & 2 & 1\\ 2 & 0 & 1 & 0\\ 0 & 2 & -3 & -2\end{matrix}\right)$$Calcoliamo il suo rango tramite la procedura bottom-up, ovvero, calcolando i determinanti degli orlati del minore $M$ nella matrice $B$ (eccetto ovviamente $A$ di cui sappiamo già essere 0):
$$\left|\begin{matrix} 1 & -1 & 1\\ 2 & 0 & 0\\ 0 & 2 & -2\end{matrix}\right|=0$$Quindi anche $r(B)=2$; per Rouché-Capelli, il sistema è possibile indeterminato con $\infty^{3-2}=\infty^1$ soluzioni. Determiniamolo attraverso i 3 step elencati sopra:
- Un minore di ordine $r=2$ a determinante non nullo l'abbiamo già individuato: $$M=\left(\begin{matrix} 1 & -1\\ 2 & 0\end{matrix}\right)$$
- Il sistema formato dalle $r=2$ equazioni corrispondenti è: $$\begin{cases} x-y+2z=1\\ 2x+z=0\end{cases}$$
- Essendo $r=2 < n=3$, determiniamo il valore delle $2$ incognite presenti nel minore $M$ scelto (ossia $x$ e $y$) in funzione delle $3-2=1$ incognite rimantenti (cioè $z$): $$\begin{cases} -\frac{z}{2}-y+2z=1\\ x=-\frac{z}{2}\end{cases}\ \Leftrightarrow \ \begin{cases} y=-\frac{z}{2}+2z-1\\ x=-\frac{z}{2}\end{cases}\ \Leftrightarrow \ \begin{cases} y=\frac{3}{2}z-1\\ x=-\frac{z}{2}\end{cases}$$
L'insieme delle $\infty^1$ soluzioni è dunque dato da:
$$S=\bigg\{\left(-\frac{z}{2},\frac{3}{2}z-1,z\right):z\in\mathbb R\bigg\}$$