Esaminiamo il seguente problema: qual è il numero positivo che elevato al quadrato dà 9?
Consideriamo di nuovo lo stesso problema, però nel campo dei numeri reali relativi.
Quali sono, se esistono, i numeri reali relativi che elavati al quadrato danno 9?
Un numero è senz'altro 3, ma non è il solo; infatti anche -3 è soluzione del problema, perchè $(-3)^2=9$.
I due numeri reali opposti, +3 e -3, si chiamano radici algebriche.
In generale,
dato il numero naturale $n\neq 0$, e un numero reale a, si chiamano radici algebriche n-esime del numero a tutti i numeri reali la cui potenza con esponente n è uguale ad a. Indichiamo ognuna di esse col simbolo $\stackrel{alg}{\sqrt[n]{a}}$
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{\sqrt[n]{a}=b\quad\Leftrightarrow\quad b^n=a\quad\quad (n\neq0,\ a,b\in\mathbb R)}$$
Calcolo radici algebriche
- La radice aritmetica $\sqrt[4]{16}$ è soltanto 2, ossia $\sqrt[4]{16}=+2$. Invece $\stackrel{alg}{\sqrt[4]{16}}=\pm 2$, perchè $(+2)^4=16$ e $(-2)^4=16$.
- La radice aritmetica $\sqrt[3]{-125}$ non esiste perchè nessun numero positivo elevato a esponente 3 può dare come risultato un numero negativo. Invece $\stackrel{alg}{\sqrt[3]{-125}}=-5$, perchè $(-5)^3=-125$.
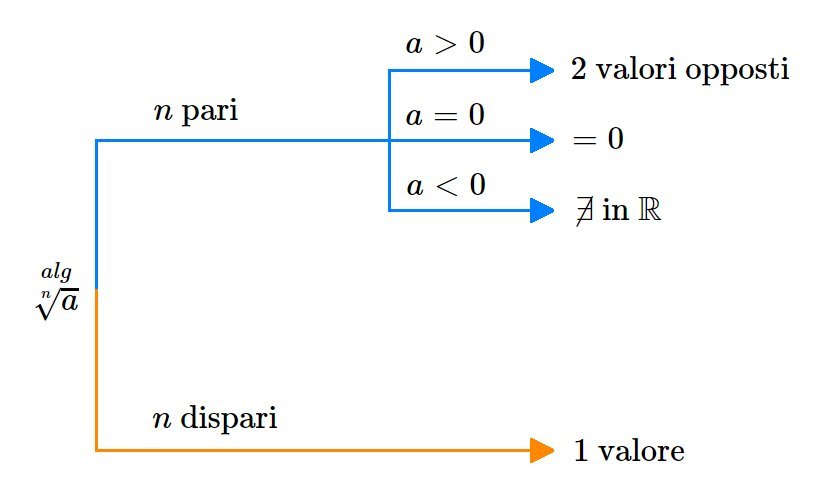
Nel campo dei numeri reali, la radice algebrica:
- se l'esponente è pari, può assumere due valori, uno oppure nessuno, a seconda che il radicando sia maggiore, uguale o minore di 0;
- se l'esponente è dispari, assume sempre un solo valore.
Calcolo radici algebriche con esponente pari
- $\stackrel{alg}{\sqrt[2]{4}}=\pm 2$.
- $\stackrel{alg}{\sqrt[4]{0}}=0$.
- $\stackrel{alg}{\sqrt[2]{-4}}$ non esiste in $\mathbb R$.
Calcolo radici algebriche con esponente dispari
- $\stackrel{alg}{\sqrt[3]{-8}}=-2$.
Il seguente diagramma fornisce una sintesi delle radici n-esime algebriche di un numero reale a.