Dopo aver specificato le ipotesi nulla e alternativa, occorre specificare quale risultato del campione porterà al rifiuto dell'ipotesi nulla.
Ricordiamo che, poichè il valore della statistica è calcolato da un campione, anche se l'ipotesi nulla è vera, è però molto probabile che tale statistica differisca di una certa quantità dal vero valore del parametro della popolazione sottoposto al test per effetto del caso. Si potrebbe confrontare il valore del parametro della popolazione con quello campionario e valutare se la loro differenza è piccola o grande per decidere se rifiutare o accettare l'ipotesi nulla. Ma il concetto di "piccola" o "grande" non sono ben definiti, per cui basiamo lo studio del test di ipotesi sulla determinazione della distribuzione campionaria di una statistica chiamata statistica test.
La statistica test è una statistica che viene calcolata dai dati del campione e può assumere diversi valori che variano in base al campione estratto.
Esempio di statistiche test sono:
$$Z=\frac{\overline{X}-\mu_0}{\frac{\sigma}{\sqrt{n}}}\quad\quad T=\frac{\overline{X}-\mu_0}{\frac{S}{\sqrt{n}}}$$
Dove $Z$ ha distribuzione normale standard, mentre $T$ ha distribuzione t di Student con n-1 gradi di libertà.
Trovato il valore della statistica test, si verifica se esso appartiene ad una regione di rifiuto o una regione di accettazione delimitate da uno o più valori detti valori critici.
La regione di rifiuto è l'insieme dei valori della statistica test che conducono al rifiuto dell'ipotesi nulla. Può essere anche vista come l'insieme dei valori della statistica test che non è probabile che si verifichino quando l'ipotesi nulla è vera, mentre è probabile che si verifichino quando l'ipotesi nulla è falsa.
La regione di accettazione è l'insieme dei valori della statistica test che conducono all'accettazione dell'ipotesi nulla.
I valori critici sono quei valori della statistica test che separano le due regioni.
Quindi, se la statistica test assume valori che cadono all'interno della regione di rifiuto, l'ipotesi nulla dovrà essere rifiutata; al contrario, l'ipotesi nulla non potrà essere rifiutata.
I test di ipotesi si dividono in due gruppi:
Test a una coda (o test unilaterale) quando la regione di rifiuto è costituita da un intervallo.
Test a due code (o test bilaterale) quando la regione di rifiuto è costituita da due intervalli, ossia da due code della distribuzione.
Per capire che tipo di test ho di fronte senza calcolare la regione di rifiuto, basta guardare l'ipotesi alternativa: se in essa è presente il $\neq$, allora si tratta di un test bilaterale, se invece compare il $<$ o il $>$, si tratta di un test unilaterale.
Errori di 1º e 2º specie
Poichè utilizziamo un campione per trarre informazioni su un'intera popolazione, il test di ipotesi effettuato può, a volte, farci giungere a conclusioni sbagliate. Gli errori che si possono commettere in questo senso sono 2:
Errore di prima specie: rifiutare $H_0$ quando $H_0$ è vera. La probabilità che questo accada è indicata con $\alpha$.
Errore di seconda specie: non rifiutare $H_0$ quando $H_0$ è falsa. La probabilità che questo accada è indicata con $\beta$.
In modo schematico avremo:
$$P(\mbox{rifiutare $H_0| H_0$ vera})=\alpha\quad\quad P(\mbox{accettare $H_0| H_0$ falsa})=\beta$$
Esempio di calcolo dell'errore di prima specie in un test unilaterale
Si vuole sottoporre a test l'affermazione di un produttore di vernici secondo cui il tempo medio di asciugatura di una nuova vernice è non superiore a $\mu=20$ minuti. A questo scopo si prende un campione di 35 lattine di vernice, si effettuano 35 prove di verniciatura con la vernice delle diverse confezioni e si calcola il tempo medio di asciugatura, con l'intenzione di rifiutare l'affermazione del produttore se la media osservata supera il valore di 20 minuti, o di accettarla in caso contrario. Da tali prove emerge che il valor medio campionario e lo scarto quadratico medio del tempo di asciugatura della vernice sono rispettivamente $\overline{X}=20,5$ e $\sigma=2$ minuti. Calcolare l'errore di prima specie.
Le ipotesi da sottoporre a test sono:
- $H_0:\mu\le 20$ minuti
- $H_1:\mu > 20$ minuti
La probabilità di commettere un errore del primo tipo è data da:
$$\alpha=P(\mbox{rifiutare $H_0| H_0$ vera})=P(\mu >20,5|\mu\le 20)$$
Sappiamo che la distribuzione della media campionaria per grandi campioni ($n\ge 30$) è approssimativamente normale, dunque la probabilità suddetta è data dall'area evidenziata in blu qui sotto.
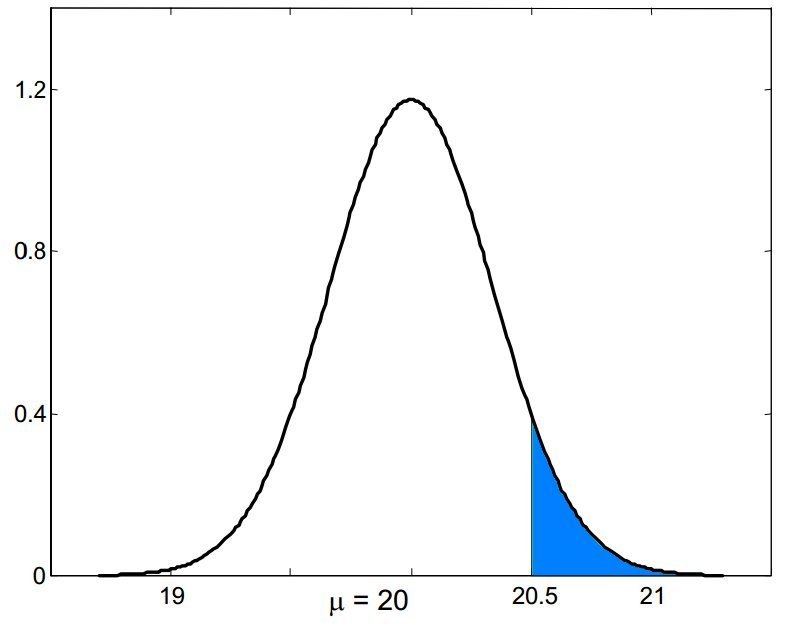
Dunque, se il valore della media campionaria cade nella regione blu l'ipotesi nulla viene rifiutata, altrimenti non viene rifiutata.
Standardizzando il valore $\overline{X}=20,5$ osservando che, per quanto detto prima, la deviazione standard della media campionaria è $\sigma_{\overline{X}}=\frac{\sigma}{\sqrt{n}}$.
$$Z=\frac{\overline{X}-\mu_0}{\frac{\sigma}{\sqrt{n}}}=\frac{20,5-20}{\frac{2}{\sqrt{35}}}=\frac{0,5}{0,34}=1,47$$
Guardando le tavole della distribuzione normale possiamo finalmente calcolarci la probabilità di rifiutare erroneamente l'ipotesi nulla è:
$$\alpha=P(Z>1,47)=1-P(Z<1,47)=1-0,9292=0,0708$$
Esempio di calcolo dell'errore di prima specie in un test bilaterale
Si vuole verificare se le lattine di caffè confezionate automaticamente da una ditta contengono in media il peso dichiarato $\mu= 250$ g. A tale scopo si estrae un campione di 30 lattine, se ne pesa il contenuto e si calcola il peso medio, per stabilire se il peso medio differisce da 250g. Si hanno i seguenti risultati: $\overline{X}=255$ g e $\sigma=15$ g. Calcolare l'errore $\alpha$ di prima specie.
Le ipotesi da sottoporre a test sono:
- $H_0:\mu= 250$ g
- $H_1:\mu\neq 250$ g
La probabilità di commettere un errore del primo tipo è data da:
$$\alpha=P(\mbox{rifiutare $H_0| H_0$ vera})=P(\mu >255|\mu= 250)$$
In questo caso, poichè il test è bilaterale, avremo due regioni di rifiuto che sono indicate in blu nella figura qui in basso.
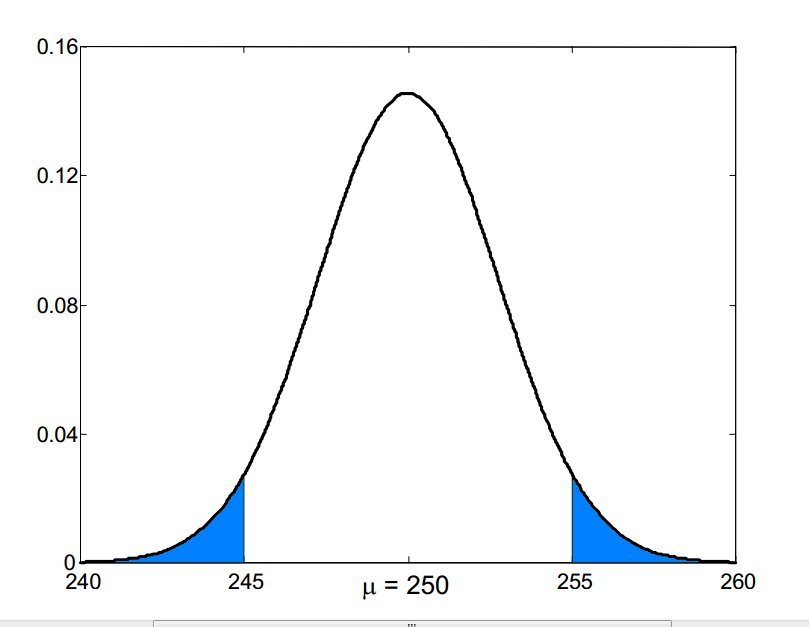
Utilizzando lo stesso procedimento fatto nell'esempio precedente, calcoliamo la statistica test:
$$Z=\frac{255-250}{\frac{15}{\sqrt{30}}}=\frac{5}{2,74}=1,82$$
L'area della regione colorata in blu e quindi la probabilità di commettere un errore di prima specie è data da:
$$\alpha=P(|Z|>1,82)=2[1-P(Z<1,82)]=2(1-0,9656)=0,0688$$
Osservazione sull'errore di seconda specie
L'errore di seconda specie $\beta$ è quantificabile solo fissando un valore per il parametro su cui si intende eseguire il test differente da quello specificato sotto l'ipotesi nulla e che sia in accordo con l'ipotesi alternativa.
Se nel primo esempio affrontato veniva richiesto di calcolare $\beta$ supposta un'ipotesi alternativa con $\mu=21,5$ minuti, avremmo calcolato la statistica test in questo modo:
$$Z=\frac{20,5-21,5}{\frac{2}{\sqrt{35}}}=\frac{-1}{0,34}=-2,94$$e dunque la probabilità di accettare $H_0$ quando essa è falsa:
$$\beta=P(Z<-2,94)=1-P(Z<2,94)=1-0.9984=0,0016$$Livello di significatività e potenza di un test
L'errore di prima specie $\alpha$ è detto pure livello di significatività oppure dimensione del test.
Nel paragrafo precedente si è discusso su come calcolare tale valore, ma questo non è il procedimento che viene usato nelle applicazioni. Di solito, infatti, il valore di $\alpha$ viene specificato prima di calcolare la regione di rifiuto.
Poichè, l'errore di primo tipo è quello considerato più grave, si preferisce sceglierlo abbastanza piccolo: i valori più utilizzati sono $\alpha=0,01$ e $\alpha=0,05$.
Il livello di significatività $\alpha$ è in relazione con il grado di fiducia introdotto per gli intevalli di confidenza:
$$\mbox{grado di fiducia}=(1-\alpha)\cdot 100\%$$
Questo significa che, se si sceglie $\alpha=0,05=5\%$, ci sarà una probabilità del 5% di rifiutare erroneamente l'ipotesi nulla; oppure, equivalentemente, siamo fiduciosi al 95% di aver preso la decisione corretta.
L'errore di seconda specie $\beta$, invece, è noto come rischio del consumatore. Da esso, possiamo ricavare la cosiddetta potenza del test:
$$\mbox{potenza del test}=1-\beta$$
che si traduce come la probabilità di rifiutare correttamente l'ipotesi nulla quando essa è falsa.
Elenchiamo alcune considerazioni utili ai fini di limitare il più possibile i due errori:
- A parità di ampiezza del campione, al diminuire di $\alpha$ aumenta $\beta$
- Per controllare e ridurre l'errore di seconda specie basta aumentare la dimensione del campione
- A parità di $\alpha$, l'aumento dell'ampiezza del campione riduce $\beta$
Inoltre, si possono dedurre le seguenti osservazioni riguardo la potenza di un test:
- Maggiore è la distanza tra ipotesi alternativa (che stiamo considerando vera) e l'ipotesi nulla, maggiore sarà la potenza del test.
- Minore è la varianza della distribuzione e maggiore sarà la potenza del test.
- Maggiore è $\alpha$, maggiore sarà la potenza del test.
- La potenza del test è influenzata dalla dimensione campionaria. A parità di $\alpha$, la varianza della distribuzione è inversamente proporzionale alla numerosità: minore è la numerosità, maggiore sarà la varianza e viceversa.
Vedi schema riassuntivo sul test di ipotesi oppure



