Il teorema della corda afferma che la misura di una corda di una circonferenza è uguale al prodotto tra la misura del diametro e il seno di uno qualunque degli angoli alla circonferenza che insistono su uno dei due archi sottesi dalla corda. In formule
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{\overline{PQ}=2r\sin\alpha=2r\sin(\pi-\alpha)}$$
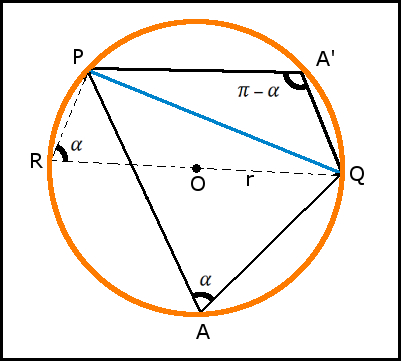
Dimostrazione
Nella figura soprastante è rappresentata una circonferenza di raggio $r$ e centro $O$ ed è tracciata una sua corda $PQ$. I punti $A$ e $A'$ appartengono rispettivamente all'arco \(\displaystyle \overset{\ \ {\displaystyle \frown}}{PQ}\) maggiore e all'arco \(\displaystyle \overset{\ \ {\displaystyle \frown}}{PQ}\) minore. Osserviamo che gli angoli $\widehat{PAQ}$ e $\widehat{PA'Q}$ sono supplementari (angoli opposti di un quadrilatero inscritto in una circonferenza) e pertanto hanno il medesimo seno.
Tracciamo il diametro avente un estremo in $Q$ e sia $R$ il suo secondo estremo. Osserviamo che gli angoli $\widehat{PRQ}$ e $\widehat{PAQ}$ sono congruenti (angoli alla circonferenza che insistono su uno stesso arco). Il triangolo $RPQ$, essendo inscritto in una semicirconferenza, è rettangolo in P pertanto per il suo cateto $PQ$ vale la relazione:
$$\overline{PQ}=\overline{QR}\sin\alpha=2r\sin\alpha$$
Ma poiché è anche, come s'è detto:
$\sin(\pi-\alpha)=\sin\alpha\quad\quad$ si ha pure $\quad\quad\overline{PQ}=2r\sin(\pi-\alpha)$
la tesi risulta dimostrata.
Determinare la misura della corda AB di una circonferenza di raggio 2, sapendo che su di essa insiste un angolo alla circonferenza di $\cfrac{\pi}{3}$
La rappresentazione grafica del problema è il seguente:
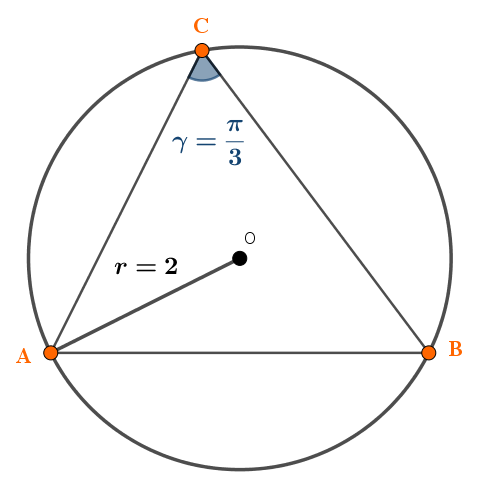
Allora, per il teorema della corda: $$\begin{array}{l}\overline{AB}=2\cdot r\cdot\sin\gamma=\\ =2\cdot 2\cdot\sin\cfrac{\pi}{3}=\\ =4\cdot\cfrac{\sqrt{3}}{2}=\\ =2\cdot\sqrt{3}\end{array}$$
Calcolo del raggio tramite il teorema della corda
Il teorema della corda consente anche di calcolare il raggio di una circonferenza circoscritta a un triangolo come in figura:
Infatti, con riferimento alla figura sopra, possiamo applicare il teorema della corda in 3 modi diversi. Cioè possiamo ricavare rispettivamente le corde $a$, $b$ e $c$:
- $a=2\cdot r\sin\alpha$
- $b=2\cdot r\sin\beta$
- $c=2\cdot r\sin\gamma$
Allora, il calcolo del raggio può avvenire in 3 modi diversi ricavando le formule inverse delle 3 appena viste che sono rispettivamente:
- $r=\cfrac{a}{2\cdot\sin\alpha}$
- $r=\cfrac{b}{2\cdot\sin\beta}$
- $r=\cfrac{c}{2\cdot\sin\gamma}$
È chiaro che l'uso di una formula piuttosto che un'altra dipende dai dati che ci fornisce il testo dell'esercizio. Qui sotto facciamo un esempio.
Calcolare il raggio della circonferenza circoscritta al triangolo ABC, di cui sono noti il lato $\overline{AB}=10$ e l'angolo $A\hat{C}B=120^{\circ}$

In questo caso basta usare la formula 3 sopra menzionata: $$\begin{array}{l}r=\cfrac{c}{2\cdot\sin\gamma}=\\=\cfrac{10}{2\cdot\sin 120^{\circ}}=\\ =\cfrac{10}{2\cdot\frac{\sqrt{3}}{2}}=\\ =\frac{10\sqrt{3}}{3} \end{array}$$




