Il teorema dei seni (o di Eulero) stabilisce una relazione tra gli elementi di un triangolo e, in particolare, afferma che in un triangolo qualunque il rapporto tra la misura di un lato e il seno dell'angolo opposto è costante.
In altre parole, indicati con $A$, $B$ e $C$ i tre vertici di un triangolo, con $\alpha$, $\beta$ e $\gamma$ i tre angoli corrispondenti, e con $a$, $b$ e $c$ le misure dei tre lati rispettivamente opposti agli angoli di vertici $A$, $B$, $C$, si possono scrivere le seguenti uguaglianze:
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{\frac{a}{\sin\alpha}=\frac{b}{\sin\beta}=\frac{c}{\sin\gamma}}$$

Dimostrazione
Il teorema dei seni si può dimostrare mediante il teorema della corda (clicca qui se vuoi ripassarlo). Infatti, se consideriamo la circonferenza circoscritta al triangolo nella figura soprastante e applichiamo a ogni lato il teorema della corda, otteniamo:
$$\begin{array}{l}a=2r\sin\alpha\\ b=2r\sin\beta\\ c=2r\sin\gamma\end{array}$$
e quindi:
$$\begin{array}{l}\cfrac{a}{\sin\alpha}=2r\\ \cfrac{b}{\sin\beta}=2r\\ \cfrac{c}{\sin\gamma}=2r\end{array}$$
Dato che i 3 rapporti sono tutti uguali a $2r$, si ha la tesi.
Calcolare la misura di AB nel triangolo ABC, considerando i dati presenti nella figura.
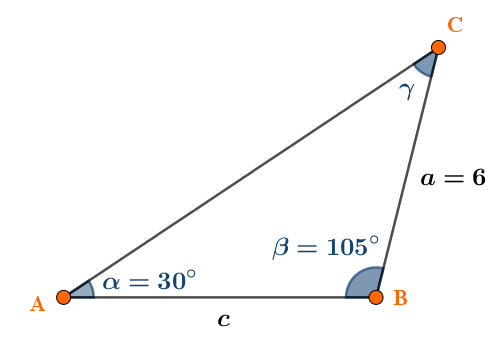
Per poter applicare il teorema dei seni è necessario calcolare l'angolo $\gamma$ sapendo che la somma degli angoli di un triangolo è $180^{\circ}$: $$\gamma=180^{\circ}-30^{\circ}-105^{\circ}=45^{\circ}$$
Adesso, utilizziamo la relazione: $\cfrac{a}{\sin\alpha}=\cfrac{c}{\sin\gamma}$ per calcolare il lato $c$:
$$\begin{array}{l}\cfrac{6}{\sin 30^{\circ}}=\cfrac{c}{\sin 45^{\circ}}\\ \cfrac{6}{\frac{1}{2}}=\cfrac{c}{\frac{\sqrt{2}}{2}}\end{array}$$
Svolgendo quest'ultima equazione, dopo alcuni passaggi ottieni $$c=6\sqrt{2}$$



