Si dice che il vettore aleatorio $(X,Y)$ ha distribuzione uniforme nel sottoinsieme $C\subseteq\mathbb R$ (e si indica con $(X,Y)\sim U_C$) se la sua densità congiunta è:
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{f(x,y)=\begin{cases} \frac{1}{mis(C)} & \mbox{se } (x,y)\in C\\ 0 & \mbox{se } (x,y)\not\in C\end{cases}}$$
dove $mis(C)$ è la misura di $C$.
Sia $C_1\subseteq C$ calcoliamo la probabilità che il vettore aleatorio appartenga all'insieme $C_1$:
$$\begin{eqnarray} P((X,Y)\in C_1) &=&\int\int_{C_1}f(x,y)\ dx\ dy=\int\int_{C_1}\frac{1}{mis(C)}\ dx\ dy\\ &=&\frac{1}{mis(C)}\int\int_{C_1}dx\ dy=\frac{mis(C_1)}{mis(C)}\end{eqnarray}$$
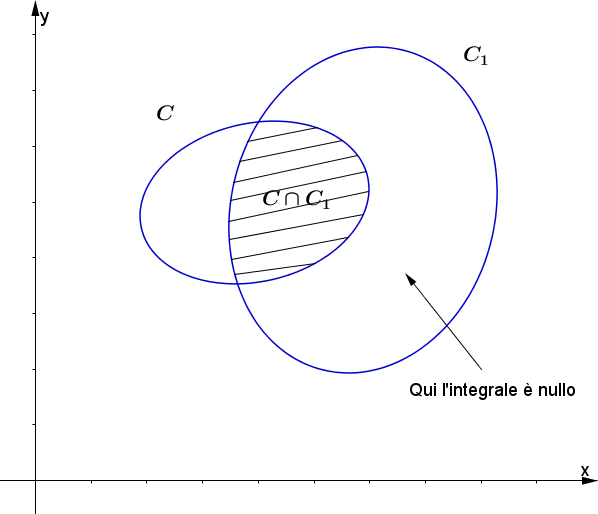
Se invece $C_1\not\subseteq C$, rifacendo il ragionamento appena fatto avremmo ottenuto:
$$P((X,Y)\in C_1)=\frac{mis(C\cap C_1)}{mis(C)}$$
Consulta altri esercizi svolti sulla distribuzione uniforme nel piano