Un test di ipotesi sulla media della popolazione può essere formulato nei seguenti tre modi: $$a)\begin{cases} H_0: \mu=\mu_0\\ H_1: \mu\neq \mu_0\end{cases} \quad b) \begin{cases} H_0: \mu\geq \mu_0\\ H_1: \mu < \mu_0\end{cases} \quad c) \begin{cases} H_0: \mu\leq \mu_0\\ H_1: \mu > \mu_0\end{cases}$$ dove il test a) è bilaterale mentre b) e c) sono unilaterali (vedi figure qui in basso).
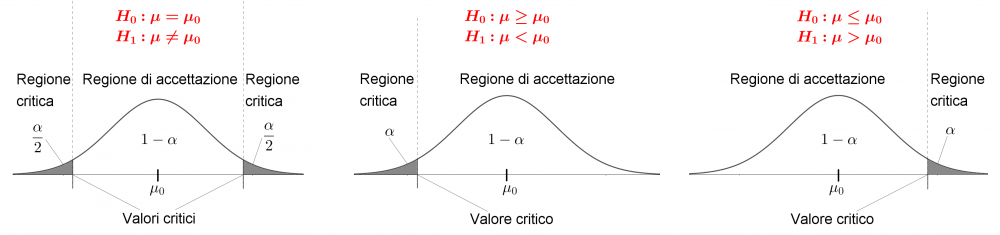
Come nel caso degli intervalli di confidenza, occorre stabilire la distribuzione dello stimatore in base alle informazioni che si hanno sulla popolazione.
A tale scopo saranno analizzati due casi:
- popolazione con distribuzione normale e varianza nota o con distribuzione qualsiasi e grandi campioni;
- popolazione con distribuzione normale, varianza incognita e piccoli campioni.
Caso popolazione normale con varianza nota o popolazione qualsiasi e grandi campioni
In questo caso, per effettuare il test, si può utilizzare la statistica test con distribuzione normale standard $$\bbox[#ffffff,5px,border:2px solid #ff6600]{Z_{test}=\frac{\overline{x}-\mu_0}{\sqrt{\frac{\sigma^2}{n}}}= \frac{\overline{x}-\mu_0}{\sqrt{\frac{s^2}{n}}}}$$
Osserviamo la doppia formula: la prima viene utilizzanda quando il campione proviene da una popolazione normale con varianza $\sigma^2$ nota; mentre invece la seconda formulazione si utilizza nel caso di un grande campione estratto da una popolazione qualsiasi (non necessariamente normale) avente varianza campionaria pari a $s^2$.
Definito il livello di significatività $\alpha$ e determinato dalle tavole il valore critico $z_{1-\alpha}$ (per i test unilaterali) e $z_{1-\frac{\alpha}{2}}$ (per i test bilaterali), L'esito del test è
- (per un test bilaterale tipo a)) rifiuto $H_0$ se $|Z_{test}| > z_{1-\frac{\alpha}{2}}$
- (per un test unilaterale sinistro tipo b)) rifiuto $H_0$ se $Z_{test} < -z_{1-\alpha}$
- (per un test unilaterale destro tipo c)) rifiuto $H_0$ se $Z_{test} > z_{1-\alpha}$
Caso popolazione normale con varianza incognita e piccoli campioni
In questo caso per effettuare il test si utilizza la statistica test con distribuzione t di Student $$\bbox[#ffffff,5px,border:2px solid #ff6600]{T_{test}=\frac{\overline{x}-\mu_0}{\sqrt{\frac{s^2}{n}}}}$$
I gradi di libertà sono $\nu=n-1$ e fissato un valore di $\alpha$ possiamo leggere dalle tavole della distribuzione t di Student il valore critico $t_{\alpha}(\nu)$ (per i test unilaterali) e $t_{\frac{\alpha}{2}}(\nu)$ (per i test bilaterali), L'esito del test è
- (per un test bilaterale tipo a)) rifiuto $H_0$ se $|T_{test}| > t_{\frac{\alpha}{2}}(\nu)$
- (per un test unilaterale sinistro tipo b)) rifiuto $H_0$ se $T_{test} < -t_{\alpha}(\nu)$
- (per un test unilaterale destro tipo c)) rifiuto $H_0$ se $T_{test} > t_{\alpha}(\nu)$



