Spieghiamo praticamente con un esempio come condurre un test di ipotesi per il quale disponiamo di due gruppi di dati dipendenti tra loro. Tale tipo di test è chiamato test t di Student per dati appaiati
Esempio
Sono stati provati due diversi sonniferi (A e B) su un campione di piccole dimensioni di pazienti affetti da insonnia. Ogni paziente ha assunto entrambi i sonniferi, l'ordine di assunzione è stato deciso in modo casuale e per ogni periodo di trattamento è stato registrato il numero medio di ore di sonno guadagnate. Verificare quale farmaco garantisce la risposta attesa migliore sapendo che i risultati delle prove sono i seguenti:
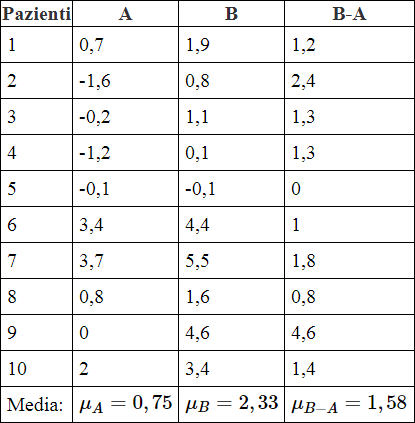
Assumiamo che le variabili risposte seguano una distribuzione normale:
$$A_i\sim N(\mu_A,\sigma_A^2)\quad\quad, B_i\sim N(\mu_B,\sigma_B^2)$$
Trattandosi di risposte osservate sullo stesso paziente è naturale considerare la loro differenza $D_i=B_i-A_i$, la quale segue anch'essa una distribuzione normale:
$$D_i\sim N(\mu_{B-A},\sigma_{B-A}^2)$$
dove $\sigma_{B-A}^2=VAR(B_i-A_i)$ è la varianza della popolazione.
Le ipotesi da sottoporre a test sono:
- $H_0:\mu_{B-A}=0$
- $H_1:\mu_{B-A}\neq 0$
Costruiamo la statistica test a partire dallo stimatore naturale del valore atteso in un modello normale, cioè la media campionaria:
$$\overline{D}=\frac{\sum\limits_{n=1}^{10} D_i}{n}=1,58$$
Ricordiamo che $\overline{D}\sim N\left(\mu_{B-A},\frac{\sigma_{B-A}^2}{n}\right)$$
dove $\sigma_{B-A}^2$ (essendo sconosciuta) può essere approssimata con la varianza campionaria $S_{B-A}^2$.
$$\sigma_{B-A}^2\simeq S_{B-A}^2=\frac{\sum\limits_{n=1}^{10}(D_i-\overline{D})^2}{n-1}=1,5129$$
Passiamo così, da una statistica distribuita normalmente ad una distribuita secondo una t di Student con n-1 gradi di libertà:
$$T_{test}=\frac{\overline{D}-\mu_{B-A}}{\frac{S_{B-A}}{\sqrt{n}}}=\frac{1,58-0}{\frac{1,23}{\sqrt{10}}}=4,062$$
Scegliendo $\alpha=0,05$, dalle tavole ricaviamo il valore critico:
$$t_{\frac{\alpha}{2},9}=t_{0,025,9}=2,262$$
Poichè $|T_{test}|=4,062 > t_{0,025,9}=2,262$ rifiutiamo l'ipotesi nulla dicendo che i due sonniferi hanno prodotto un effetto differente sui pazienti.



