Si definisce numero indice o rapporto di variazione il rapporto tra l'intensità di un fenomeno in un certo periodo di tempo e l'intensità dello stesso fenomeno in un altro periodo diverso dal precedente. Tale definizione ci fa capire che i numeri indici servono per studiare la variazione che subisce l'intensità di un fenomeno in una serie storica da un periodo di tempo a un altro. Se non lo sapessi una serie storica o temporale è una sequenza di osservazioni, relative a un certo fenomeno, effettuate in $T$ tempi (mesi, anni, ecc.). Un esempio di serie storica può essere l'andamento del PIL in un certo arco di tempo.
Esistono 2 tipi di numeri indici:
- numeri indice a base fissa: si calcolano come rapporto tra l'intensità di un fenomeno al tempo $t$ e quella al tempo $b$ (tempo base): $$\bbox[#ffffff,5px,border:2px solid #ff6600]{I_{t/b}=\frac{x_t}{x_b}\cdot 100\%}$$
- numeri indice a base mobile: si calcolano come rapporto tra l'intensità di un fenomeno al tempo $t$ e quella al tempo $t-1$ (tempo precedente): $$\bbox[#ffffff,5px,border:2px solid #ff6600]{i_t=\frac{x_t}{x_{t-1}}\cdot 100\%}$$
Inoltre, si può calcolare la variazione percentuale del fenomeno dal tempo $t-1$ al tempo $t$, come il rapporto percentuale tra la variazione assoluta al tempo $t$ e l'intensità al tempo $t-1$: $$\bbox[#ffffff,5px,border:2px solid #ff6600]{v_t=\frac{x_t-x_{t-1}}{x_{t-1}}\cdot 100\%=\left(\frac{x_t}{x_{t-1}}-1\right)\cdot 100\%=i_t\cdot 100\%-100\%}$$
Esempio
Determina i numeri indice a base fissa (anno 2011) e a base mobile e la variazione percentuale della seguente serie storica delle richieste di cittadinanza:
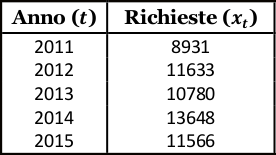
Calcoliamo dapprima i numeri indice a base fisse (2011): $$\begin{eqnarray} I_{11/11}&=&\frac{x_{11}}{x_{11}}\cdot 100\%=\frac{8931}{8931}\cdot 100\%=100\%\\ I_{12/11}&=&\frac{x_{12}}{x_{11}}\cdot 100\%=\frac{11633}{8931}\cdot 100\%=130.25\%\\ I_{13/11}&=&\frac{x_{13}}{x_{11}}\cdot 100\%=\frac{10780}{8931}\cdot 100\%=120.70\%\\ I_{14/11}&=&\frac{x_{14}}{x_{11}}\cdot 100\%=\frac{13648}{8931}\cdot 100\%=152.82\%\\ I_{15/11}&=&\frac{x_{15}}{x_{11}}\cdot 100\%=\frac{11566}{8931}\cdot 100\%=129.50\%\end{eqnarray}$$ e poi quelli a base mobile: $$\begin{eqnarray} i_{12}&=&\frac{x_{12}}{x_{11}}\cdot 100\%=\frac{11633}{8931}\cdot 100\%=130.25\%\\ i_{13}&=&\frac{x_{13}}{x_{12}}\cdot 100\%=\frac{10780}{11633}\cdot 100\%=92.67\%\\ i_{14}&=&\frac{x_{14}}{x_{13}}\cdot 100\%=\frac{13648}{10780}\cdot 100\%=126.60\%\\ i_{15}&=&\frac{x_{15}}{x_{14}}\cdot 100\%=\frac{11566}{13648}\cdot 100\%=84.75\%\end{eqnarray}$$
Infine le variazioni percentuali: $$\begin{eqnarray} v_{12}&=& i_{12}\cdot 100\%-100\%=30.25\%\\ v_{13}&=& i_{13}\cdot 100\%-100\%=-7.33\%\\ v_{14}&=& i_{14}\cdot 100\%-100\%=26.60\%\\ v_{15}&=& i_{15}\cdot 100\%-100\%=-15.25\%\end{eqnarray}$$
Il tutto è sintetizzato nella seguente tabella:

Interpretazione statistica dei numeri indici
Supponiamo di aver calcolato il numero indice a base mobile del PIL italiano per l'anno 2022 e supponiamo che sia risultato 101,46%. Per interpretarlo sottrai prima 100: $$101,46-100=1,46\%$$ Questo ci dice che nell'anno 2022 il PIL ha subito un aumento del 1,46% rispetto all'anno precedente.
Se invece il PIL fosse risultato 97,5% allora calcolando $$97,5-100=-2,5\%$$ otterremo una diminuzione del PIL del 2,5% rispetto all'anno precedente.
Differenze prime, seconde, terze, ecc
Nello studio delle serie temporali è talvolta richiesta la trasformazione in differenze del fenomeno o variabile $x$.
Le differenze prime di $x$ al tempo $t$ sono le differenze tra l'intensità del fenomeno al tempo $t$ e quelle al tempo precedente $t-1$: $$\Delta x_t=x_t-x_{t-1}$$
Le differenze seconde di $x$ al tempo $t$ sono le differenze tra la differenza prima al tempo $t$ e quella al tempo precedente $t-1$: $$\Delta^2 x_t=\Delta x_t-\Delta x_{t-1}$$
Le differenze terze di $x$ al tempo $t$ sono le differenze tra la differenza seconda al tempo $t$ e quella al tempo precedente $t-1$: $$\Delta^3 x_t=\Delta^2 x_t-\Delta^2 x_{t-1}$$
Con riferimento all'esercizio precedente, calcoliamo le differenze prime e seconde di $x_15$ (ossia delle richieste di cittadinanza relative all'anno 2015).
Per prima cosa calcoliamo le differenze prime per i periodi 2014 e 2015
$$\begin{eqnarray}\Delta x_{15}&=&x_{15}-x_{14}=\\ &=&11566-13648=\\ &=&-2082\\ \Delta x_{14}&=&x_{14}-x_{13}=\\ &=&13648-10780=\\ &=&2868\end{eqnarray}$$
Adesso calcoliamo la differenza seconda riferita al periodo 2015: $$\begin{eqnarray}\Delta^2 x_{15}&=&\Delta x_{15}-\Delta x_{14}=\\ &=&-2082-2868=\\ &=&-4950\end{eqnarray}$$



