Questa è una lezione di raccordo con il programma di quinta elementare. Infatti, spiegheremo e approfondiremo le quattro operazioni fondamentali della matematica, ossia addizione, sottrazione, moltiplicazione e divisione.
L'addizione
L'addizione è l'operazione che fa corrispondere a due numeri un terzo numero, ottenuto contando di seguito al primo tante unità quante ne indica il secondo.

I numeri $3$ e $4$ dell'esempio precedente si dicono addendi dell'addizione, il numero $7$, risultato dell'operazione, si dice somma.

Consideriamo ora i seguenti esempi: $21+0$ e $0+21$.
Osservazione:
In un'addizione, se uno dei due addendi è zero la somma è uguale all'altro addendo. Per questo motivo il numero zero è detto elemento neutro dell'addizione.
L'addizione in colonna
Quando gli addendi sono molti conviene effettuare l'addizione disponendo gli addendi in colonna. Si dispongono le cifre degli addendi incolonnandole secondo il loro valore posizionale; si sommano quindi le cifre dello stesso ordine partendo dalla colonna più a destra stando attenti, se il risultato parziale supera il $9$, a trasportare il "riporto" nella colonna dell'ordine successivo.
Esempio di addizione in colonna
Eseguiamo l'addizione
$$3457+312+7+8608$$Avremo dunque:
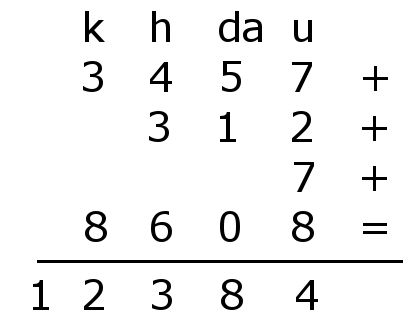
Calcolare le seguenti addizioni:
- $29+1+11+5$.
- $59+28+61+12$.
- $2741+359+259+41$.
La sottrazione
La sottrazione è l'operazione che fa corrispondere a due numeri un terzo numero, che addizionato al secondo dà per risultato il primo.
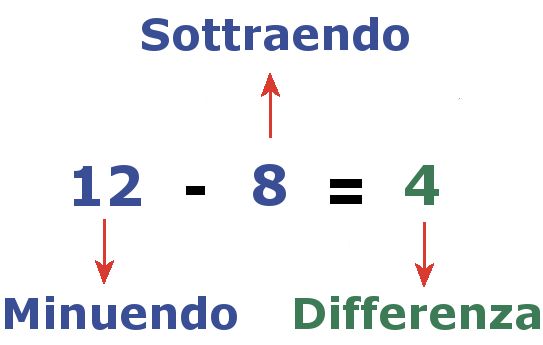
$$12-8=4\quad\quad\mbox{perchè}\quad\quad 4+8=12$$ 
I numeri $12$ e $8$ dell'esempio precedente si dicono rispettivamente minuendo e sottraendo; il numero $4$, risultato dell'operazione, si dice differenza o resto. Per quanto detto è anche evidente che la sottrazione è l'operazione inversa dell'addizione.
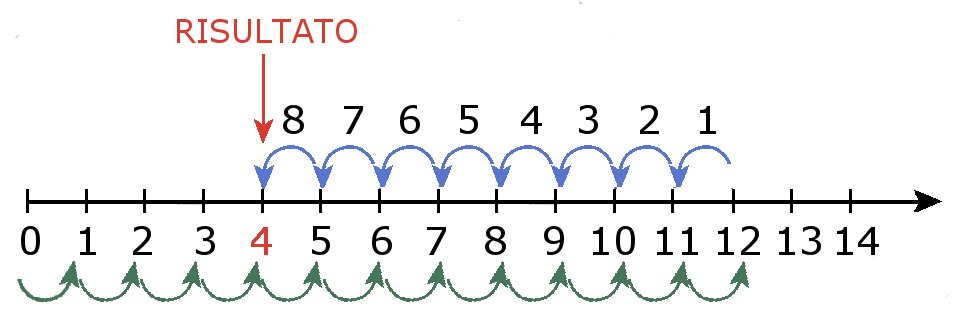
Possiamo eseguire la sottrazione fra i numeri $12$ e $8$ anche utilizzando la semiretta dei numeri. Dobbiamo partire da zero e spostarci verso destra di $12$ unità (archi in verde). A questo punto dovremo spostarci verso sinistra (verso lo zero) di tante unità quante quelle del secondo numero cioè $8$ (archi in azzurro): in questo modo otteniamo il punto immagine del numero $4$.
Osserviamo che non è possibile svolgere l'operazione della sottrazione con qualsiasi coppia di numeri naturali. Ad esempio, non possiamo calcolare la differenza $5-7$ perchè nessun numero naturale, addizionato a $7$, dà come risultato $5$. Nel programma di seconda media scopriremo che è possibile svolgere l'operazione $5-7$ introducendo i numeri interi relativi:
La sottrazione in colonna
Come per l'addizione, è opportuno eseguire le sottrazioni di una certa complessità mediante il metodo dell'operazione in colonna.
Anche in questo caso bisogna incolonnare una sotto l'altra le unità dello stesso ordine e iniziare a sottrarre le cifre a partire da quelle più a destra. Nel seguenti esempi abbiamo indicato con un corpo più piccolo i numeri del riporto.
Esempio di sottrazione in colonna
Eseguiamo in colonna la seguente sottrazione:
$$7459-789$$
Calcolare le seguenti sottrazioni:
- $816-318$.
- $2741-1799$.
- $745-150-322$.
La moltiplicazione
La moltiplicazione è l'operazione che fa corrispondere a due numeri un terzo numero, ottenuto eseguendo l'addizione di tanti addendi uguali al primo, quanti ne indica il secondo.
I numeri $6$ e $4$ dell'esempio precedente si dicono rispettivamente moltiplicando e moltiplicatore oppure 1° e 2° fattore; il risultato dell'operazione, si dice prodotto o resto.
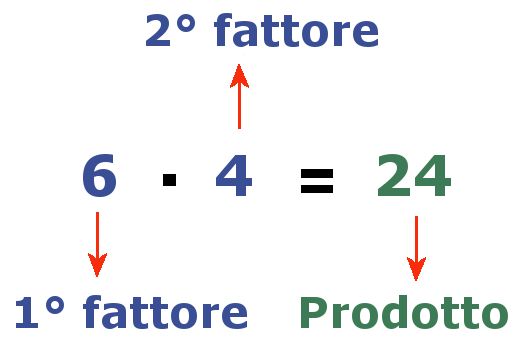
Consideriamo ora i prodotti: $22\cdot 1=22$ e $1\cdot 22=22$.
Osservazione
In una moltiplicazione se uno dei due fattori è il numero $1$ il prodotto è uguale all'altro fattore. Per questo il numero $1$ è l'elemento neutro della moltiplicazione.
Consideriamo il prodotto $0\cdot 5$. Dobbiamo sommare tanti addendi uguali al primo quanti ne indica il secondo:
$$\underbrace{0+0+0+0+0}_{\mbox{5 volte}}=0\quad\quad\mbox{quindi}\quad\quad 0\cdot 5=0$$
In modo analogo possiamo anche dire che $5\cdot 0=0$.
Osservazione
Il prodotto di due fattori è uguale a zero se e solo se almeno uno dei fattori è uguale a zero. Il numero $0$ è detto elemento assorbente della moltiplicazione.
La moltiplicazione in colonna
Per eseguire una moltiplicazione in colonna basta tenere presente che ogni cifra del moltiplicatore deve essere moltiplicata per ogni cifra del moltiplicando; i risultati parziali vengono scritti in colonna e alla fine sommati.
Esempio di moltiplicazione in colonna
Eseguiamo in colonna la seguente moltiplicazione:
$$363\cdot 215$$
Calcolare le seguenti moltiplicazioni:
- $12\cdot 86$.
- $14\cdot 144$.
- $1764\cdot 849$.
La divisione
La divisione è l'operazione che fa corrispondere a due numeri, di cui il secondo diverso da zero, un terzo numero, se esiste, che moltiplicato per il secondo dà come risultato il primo
$$15:3=5\quad\quad\mbox{perchè}\quad\quad 5\cdot 3=15$$ 
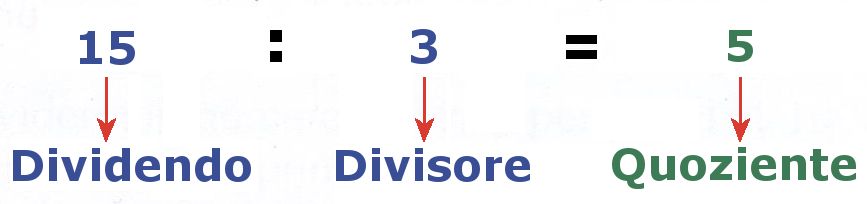
I numeri $15$ e $3$ dell'esempio precedente si dicono rispettivamente dividendo e divisore e il numero $5$, risultato dell'operazione, si dice quoto o quoziente. Per quanto detto è anche evidente che la divisione è l'operazione inversa della moltiplicazione.
Osserviamo che non sempre il risultato di una divisione è esatto. Consideriamo infatti la divisione $15:6$. Si ha:
$$15:6=2\quad\quad\mbox{con resto}\quad 3.$$
In divisioni di questo tipo il quoto si dice approssimato perchè il prodotto di quest'ultimo con il divisore non dà come risultato il dividendo, ma un numero ad esso inferiore. Per ottenere come risultato il dividendo è necessario aggiungere, al precedente prodotto, il resto:
$$\mbox{quoto}\cdot \mbox{divisore}+\mbox{resto}=\mbox{dividendo}$$
L'applicazione di questa formula consente la verifica del risultato ottenuto nell'esecuzione della divisione. Viene anche detta prova della divizione. Nel nostro caso:
$$6\cdot 2+3=15$$
La divisione in colonna
Esempio di divisione in colonna:
Risolviamo la seguente divisione:
$$255:15$$
Calcolare le seguenti divisioni:
- $130:6$.
- $892:8$.
- $7450:25$.



