In geometria si studiano degli oggetti noti come enti geometrici fondamentali dai quali è possibile costruire tutti gli altri oggetti. Essi sono:
- punto: quello che disegnamo sul foglio è solo una rappresentazione dell'idea che abbiamo del punto. Il punto ideale non ha dimensione, mentre quello che disegnamo con la matita, per quanto piccolo, ha un'estensione.
- retta: anche la retta che disegnamo sul foglio è la rappresentazione dell'idea di una retta. Quella che disegnamo è una parte di retta e ha per forza uno spessore, mentre la retta ideale è illimitata da entrambe le parti e non ha spessore.
- piano: il piano ideale è illimitato in tutte le direzioni. Possiamo disegnare sul foglio solo una parte che lo rappresenta.

Un insieme qualsiasi di punti costituisce una figura geometrica; lo spazio è l'insieme di tutti i punti e contiene quindi tutte le figure. Una figura che appartiene a un piano si chiama figura piana, altrimenti si chiama figura solida. In questo capitolo tratteremo solo figure piane.
Come detto, da questi tre enti geometrici fondamentali, ne nascono altri. Essi sono:
- semiretta: l'insieme formato da un suo punto O detto origine e dai punti che lo seguono o lo precedono. La definizione afferma che su una retta esistono due semirette opposte, con la stessa origine.

- segmento: l'insieme dei punti di una retta compresi tra due suoi punti A e B. A e B si chiamano estremi del segmento.

- poligonale: figura costituita da un insieme ordinato di segmenti in cui ciascun segmento e il successivo siano consecutivi.

- semipiano: porzione di piano costituita da una retta (detta origine del semipiano) e da una delle due regioni in cui il piano è diviso dalla retta stessa.

- angolo: ciascuna delle due parti di un piano individuate da due semirette aventi la stessa origine (O detto vertice dell'angolo), incluse le due semirette

Angoli e misure
Gli angoli si distinguono in base alla loro ampiezza:
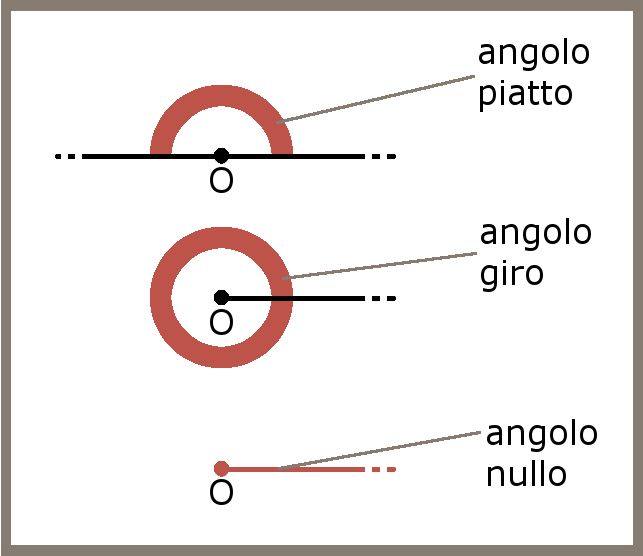
- angolo piatto: un angolo è piatto quando i suoi lati sono due semirette opposte.
- angolo giro: l'angolo i cui lati sono semirette coincidenti e che coincide con l'intero piano.
- angolo nullo: un angolo è nullo quando i suoi lati sono due semirette coincidenti e non comprende altri punti oltre quelli dei lati.
- angolo retto: ogni angolo metà di un angolo piatto.

- angolo acuto: ogni angolo minore di un angolo retto.
- angolo ottuso: ogni angolo maggiore di un angolo retto.

- angoli supplementari: due angoli sono supplementari se la loro somma è un angolo piatto.
- angoli complementari: due angoli sono complementari se la loro somma è un angolo retto.
Le proprietà delle figure
Le figure geometriche vengono classificate in base alle seguenti proprietà:
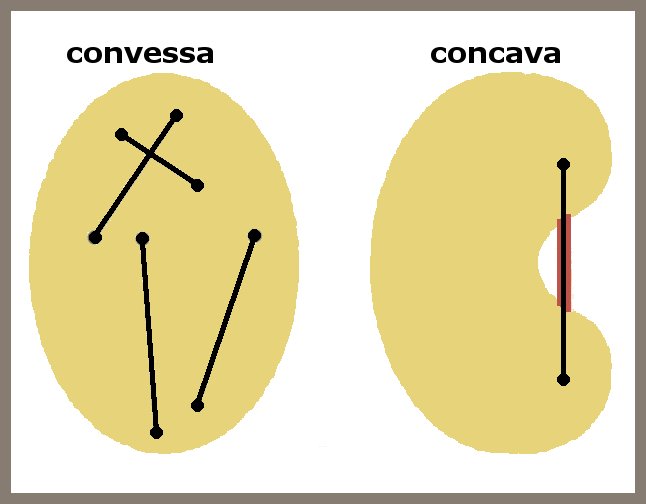
- figura convessa: una figura è convessa se due suoi punti qualsiasi sono estremi di un segmento che appartiene interamente alla figura stessa.
- figura concava: una figura è concava se non è convessa ovvero, se almeno due dei suoi punti sono estremi di un segmento che non appartiene interamente alla figura.
- figure congruenti: due figure sono congruenti se sono sovrapponibili punto a punto l'una sull'altra mediante un movimento rigido (cioè un movimento che non le deformi)