Il teorema di Pitagora afferma che in un triangolo rettangolo, il quadrato costruito sull'ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti.
In formule:
$$c^2=b^2+h^2$$ 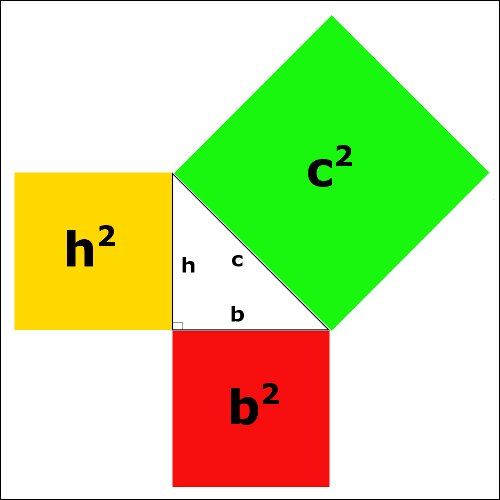
Ricordiamo che un triangolo rettangolo è un poligono composto da tre lati (in generale diversi) e da tre angoli di cui uno retto ($90^°$). La base e l'altezza vengono chiamati cateti, mentre il lato obliquo ipotenusa

Formule inverse
Dal teorema di Pitagora si ricavano le seguenti formule per un triangolo rettangolo:
- Base con altezza e ipotenusa note:$\quad b=\sqrt{c^2-h^2}$
- Altezza con base e ipotenusa note:$\quad h=\sqrt{c^2-b^2}$
- Ipotenusa con altezza e base note:$\quad c=\sqrt{b^2+h^2}$
Dimostrazione del Teorema di Pitagora
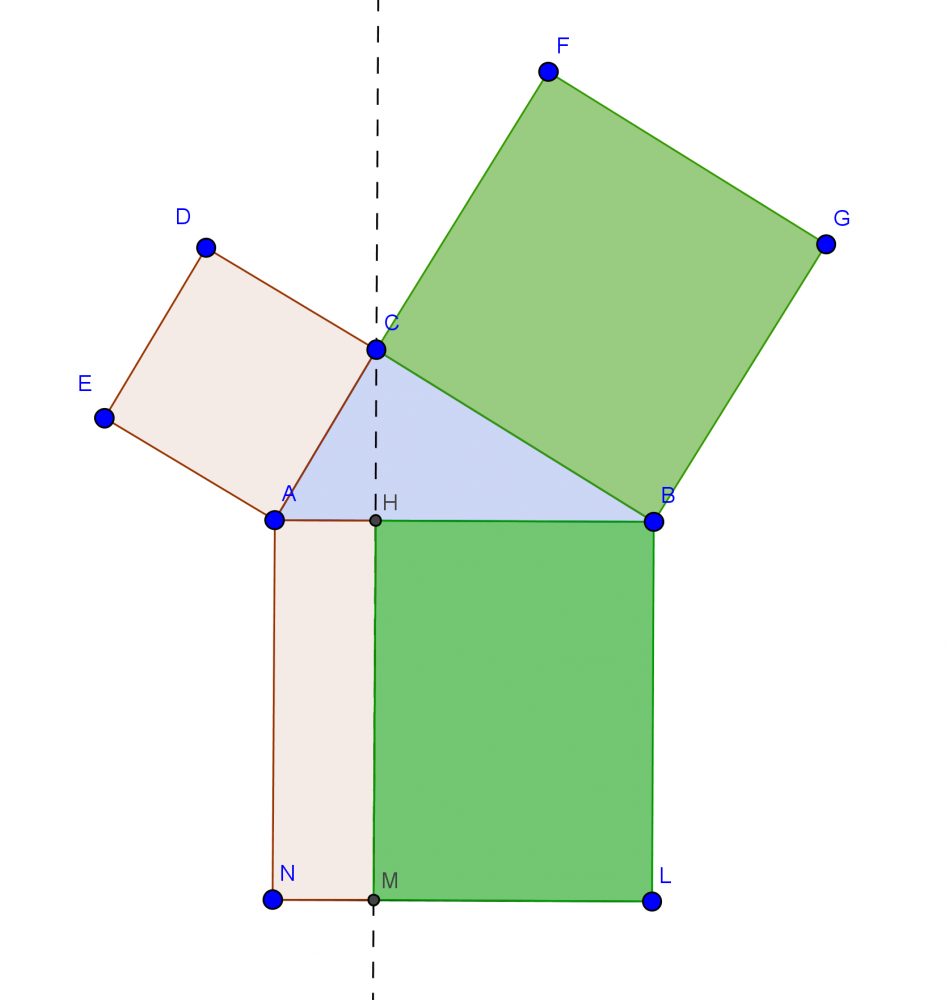
Consideriamo il triangolo rettangolo $ABC$ rettangolo in $\hat{C}$. Vogliamo dimostrare che la somma dei quadrati costruiti sui due cateti ($q(AC) + q(BC)$) è equivalente al quadrato costruito sull'ipotenusa $q(AB)$.
$$\mbox{IPOTESI:}\quad\begin{array}{l} 1)\ ABC \ \mbox{ rettangolo in } \ \hat{C} \end{array}\quad\Rightarrow\quad\mbox{TESI:}\quad\begin{array}{l} q(AC) + q(BC) \doteq q(AB) \end{array}$$
DIMOSTRAZIONE
Conduciamo la perpendicolare $CH$ dal vertice $C$ all'ipotenusa $AB$ e prolunghiamola fino a incontrare in $M$ il lato $NL$ del quadrato costruito sull'ipotenusa.
Il segmento $HM$ divide il quadrato costruito sull'ipotenusa in due rettangoli che, per il primo Teorema di Euclide, risultano equivalenti ai rispettivi quadrati costruiti sui cateti: cioè $AHMN \doteq ACDE$ e $HBML \doteq BCGF$. Osservando, quindi, che la somma dei due rettangoli dà il quadrato costruito sull'ipotenusa, resta provato il teorema.



