La termologia o calorimetria è quella branca della fisica che studia gli scambi di calore tra i corpi e fornisce metodi di misura della temperatura e delle scale di riferimento.
Innanzitutto partiamo dalla definizione di calore.
Il calore, come il lavoro, rappresenta una forma di energia; infatti, possiamo aumentare la temperatura di una sostanza fornendole calore oppure lavoro meccanico. Ad esempio, il fisico James Prescott Joule dimostrò che per aumentare la temperatura di 1 grado Kelvin (o gradi centigradi) di 1kg di acqua occorrono 4180J di lavoro.
Per arrivare a ottenere l'equazione fondamentale della termologia bisogna prima introdurre la capacità termica e il calore specifico.
La capacità termica C è il rapporto tra l'energia che acquista una sostanza e l'aumento di temperatura: $$C=\frac{\Delta E}{\Delta T}\quad (1)$$
e si misura in $\frac{J}{K}$ o $\frac{J}{°C}$. Specifichiamo che $\Delta E$ è la variazione di energia che acquista la sostanza ed è data dalla differenza tra l'energia finale e quella iniziale ($\Delta E=E_f-E_i$). Analogamente $\Delta T$ è la sua variazione di temperatura data da $\Delta T= T_f-T_i$.
Esempio
Supponiamo che fornendo 4000J di calore ad una certa quantità di acqua, la temperatura aumenta di 3°C (gradi centigradi). Allora la sua capacità termica vale: $$C=\frac{4000}{3}=1333.33\frac{J}{K}$$
Si definisce invece calore specifico quella costante che caratterizza ciascuna sostanza, data dal rapporto tra la capacità termica e la sua massa: $$c=\frac{C}{m}\quad \bigg[\frac{J}{kg\cdot K}\bigg] \quad (2)$$
In altre parole, il calore specifico rappresenta la quantità di energia che 1kg di sostanza deve acquistare affinché la sua temperatura aumenti di 1K. Di conseguenza, maggiore è la massa che dobbiamo riscaldare, tanto maggiore è l'energia necessaria per far aumentare la temperatura.
Qui in basso è presente una tabella contenente i valori specifici medi di alcune sostanze, quali l'acqua, il ghiaccio, l'alluminio, il vetro, il ferro, il rame, ecc.

Siamo pronti per scrivere la formula fondamentale della termologia che si ricava da (1) e $(2)$: $$\bbox[#ffffff,5px,border:2px solid #ff6600]{\Delta E=c\cdot m\cdot\Delta T}\quad (\large\star)$$
Tale formula ci dice che l'energia scambiata è direttamente proporzionale alla massa della sostanza e alla variazione di temperatura, oltre a essere legata alla natura della sostanza (attraverso il calore specifico c).
Negli esercizi di termologia, molto spesso l'energia viene fornita sotto forma di calore Q. In tal caso la ($\large\star$) diventa: $$Q=c\cdot m\cdot\Delta T$$
L'equilibrio termico
La temperatura di equilibrio $T_e$ è quella temperatura che due corpi, inizialmente aventi temperature diverse, raggiungono trascorso un tempo t dall'istante in cui vengono messi a contatto.
Per capire fisicamente cosa succede, consideriamo il seguente sistema termodinamico formato da due corpi accostati l'uno accanto all'altro e aventi rispettivamente massa $m_1$ ed $m_2$ e temperature iniziali $T_1$ e $T_2$:
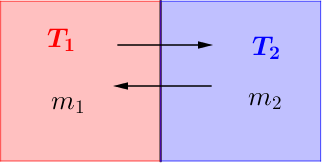
Supponiamo che il corpo di massa $m_1$ è quello più caldo, dunque si ha $T_1>T_2$. Dal momento in cui i due corpi vengono messi a contatto, si verificherà uno scambio di calore bidirezionale; il corpo più caldo cede calore a quello più freddo: $$Q_{ceduto}=m_1\cdot c_1\cdot (T_e-T_1)$$
Di conseguenza il corpo più freddo riceve calore dal corpo più caldo: $$Q_{acquistato}=m_2\cdot c_2\cdot (T_e-T_2)$$
Osserviamo che il calore ceduto è negativo poiché la variazione di temperatura $T_e-T_1 < 0$ ($T_1 > T_e$), mentre il calore acquistato è positivo dato che $T_e-T_2 > 0$. Inoltre, se non ci sono dispersioni di calore nell'ambiente o verso altre sostanze, tutto il calore ceduto da $m_1$ viene completamente acquistato da $m_2$, per cui vale: $$Q_{acquistato}=-Q_{ceduto}$$
Sostituendo le espressioni dei calori precedentemente trovare, otteniamo l'equazione dell'equilibrio termico in assenza di dispersione di calore: $$m_2\cdot c_2\cdot (T_e-T_2)=-m_1\cdot c_1\cdot (T_e-T_1)$$
Nelle applicazioni, tale equazione è utile per calcolare, ad esempio, la temperatura di equilibrio. Facendo alcuni passaggi si ottiene: $$T_e=\frac{m_1\cdot c_1\cdot T_1+m_2\cdot c_2\cdot T_2}{m_1\cdot c_1 + m_2\cdot c_2}$$



