Campo elettrico generato da una particella
Il concetto di campo elettrico è legato all'interazione elettrica che si crea tra una particella carica $Q$ e un punto $P$ nello spazio.
Se nel punto $P$ mettessimo una carica $q$, indicata con $r$ la sua distanza rispetto alla carica $Q$, abbiamo visto che per la legge di Coulomb(INSERIRE LINK), la carica $q$ subirebbe la forza elettrostatica $$F_{es}=\frac{kQ\cdot q}{r^2}$$ con $k=\frac{1}{4\pi \varepsilon_0}$.
Definiamo campo elettrostatico in un punto $P$ dello spazio il vettore $\vec{E}$ il cui modulo è: $$\bbox[#ffffff,5px,border:2px solid #ff6600]{|\vec{E}|=\frac{kQ}{r^2}}$$
Da tale formula si può osservare che il campo elettrico non dipende dalla carica di prova $q$ posta nel punto $P$, ma solo dalla carica $Q$ che lo genera e dalla distanza dal punto $P$.
Osserviamo, inoltre, che mettendo in relazione le precedenti due formule (forza elettrostatica e campo elettrico), otteniamo una formula alternativa per il calcolo del campo elettrico: $$\bbox[#ffffff,5px,border:2px solid #ff6600]{|\vec{E}|=\frac{\vec{F_{es}}}{q}}$$ dalla quale si evince l'unità di misura del campo elettrico: $\frac{N}{C}$.
Per convenzione si sceglie il verso del campo elettrico tenendo conto del segno della carica $Q$: se la carica $Q$ è positiva, il campo elettrico avrà lo stesso verso del vettore posizione $\vec{r}$: 
altrimenti, se la carica $Q$ è negativa, il campo elettrico ha verso opposto a quello di $\vec{r}$: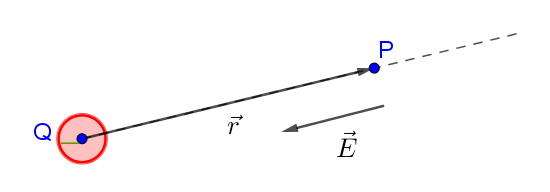 
Per una visione più vicina alla realtà del campo elettrico, possiamo disegnare le cosiddette linee di forza del campo, ossia delle linee che definiscono la direzione e il verso del campo elettrico nella porzione di spazio considerata. Ad esempio, qui sotto abbiamo graficato il campo elettrico attorno a una carica positiva e attorno ad una carica negativa. In entrambi i casi il campo elettrico è radiale (verso l'esterno nel primo caso e verso l'interno nel secondo).
Esempio calcolo del campo elettrico di una carica puntiforme
Ricordando che il modulo del campo elettrostatico generato da una carica $Q$ in un punto posto a distanza $r$ è dato da:
$$E = \frac{F}{q} = \frac{1}{4 \pi \epsilon_0} \frac{Q}{r^2}$$ basta sostituire $Q =4 \cdot 10^{-9}$ e $r= 1$ ottenendo: $$E = 9 \cdot 10^{9} \cdot 4 \cdot 10^{-9} = 36 \frac{N}{C}$$ Per il secondo punto basta ricordare la definizione di campo elettrico $\vec{E} = \frac{\vec{F}}{q}$ e ricavare quindi che la forza che il campo elettrico esercita su una carica di prova $q$ è $$\vec{F} = q \cdot \vec{E}$$
Nel caso specifico, per trovare il suo modulo basterà andare a sostituire i valori di $E = 36 \frac{N}{C}$ e $q= 2 \cdot 10^{-9} C$ : $$F = 2 \cdot 10^{-9} \cdot 36 = 72 \cdot 10^{-9} N$$
Campo elettrico generato da una distribuzione discreta di cariche
Se invece di una particella avessimo una distribuzione discreta di particelle, ovvero una quantità numerabile di particelle cariche, il campo elettrico in un punto $P$ dello spazio sarà la somma dei campi elettrici generati da ciascuna particella: $$\vec{E}=\sum_i\vec{E_i}$$
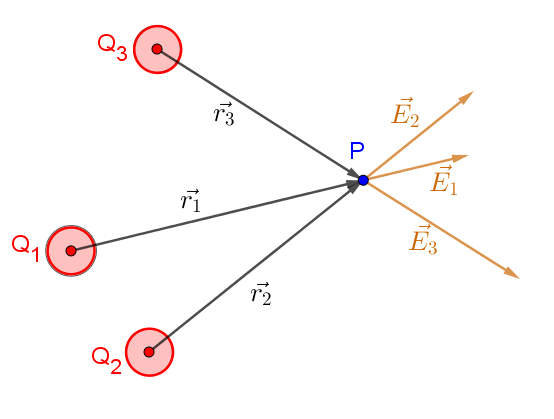
Il disegno sopra mostra i vettori campo elettrico $E_i$ nel caso in cui le particelle sono cariche positivamente. Chiaramente, il vettore campo elettrico somma sarà quel vettore che ha come componente orizzontale e verticale rispettivamente la somma delle componenti orizzontali e verticali dei singoli $E_i$. Qui sotto riportiamo la rappresentazione del vettore campo elettrico somma nel caso di due particelle.
Nella prima figura è rappresentato il vettore campo elettrico $\vec{E}$ generato da due cariche positive $+Q_1$, e $+Q_2$ su un punto $P$ (che funge da carica di prova). Negli altri due casi, abbiamo situazioni analoghe ma con cariche di segno diverso.
Anche in questo caso possiamo rappresentare le linee di forza di una distribuzione discreta di carica. Per comodità rappresentiamo le linee di forza di un dipolo elettrico, ossia una struttura formata da due cariche aventi stessa intensità ma segno opposto:
Esempio calcolo del campo elettrico di una distribuzione discreta di cariche
Per calcolare la forza che agisce su una delle cariche, ad esempio su $q_3$, calcoliamo i campi $E_1$ e $E_2$ prodotti da $q_1$ e $q_2$ nel punto $q_3$ ($q_3$ funge da carica di prova). Essendo $q_3$ equidistante da $q_1$ e $q_2$, si ha: $$E_1=E_2=\frac{kq}{l^2}$$
I due campi sono disposti simmetricamente rispetto l'asse y e quindi le loro componenti lungo l'asse x si annullano nella somma (essendo uguali e opposte); invece le componenti lungo l'asse y, uguali e concordi, si ottengono applicando i teoremi sui triangoli rettangoli: $$E_{1x}=E_{2x}=\frac{k\cdot q\cdot cos30°}{l^2}$$
La loro somma darà il modulo del campo elettrico totale agente su $q_3$: $$E=E_{1x}+E_{2x}$$
Il modulo della forza $F$ che agisce su $q_3=q$ vale $$F=q_3\cdot E=q_3\cdot\frac{k\cdot q\cdot cos30°}{l^2}$$
Il vincolo che tiene ferma ciascuna carica deve esercitare una forza uguale a opposta. Poichè il centro di un triangolo equilatero è equidistante da tutti e tre i vertici, i moduli dei campi elettrici generati dalle tre cariche nel punto C sono uguali. Dunque, il campo elettrico nel punto C dato dalla somma dei tre campi elettrici è nullo: $$E=E_1+E_2+E_3=0$$
Osserviamo che se ponessimo in C una carica, essa non risentirebbe di alcuna forza e resterebbe in equilibrio.
Campo elettrico generato da una distribuzione continua di cariche
Una distribuzione continua $V$ di carica è una struttura in cui le particelle non sono concentrate in un punto ma sono presenti un pò dappertutto. In questo caso, si considera una porzione $dV$ dell'oggetto carico (vedi figura in basso); identificando con $dq$ la piccola porzione di carica di tale frammento, il campo elettrico in un punto $P$, analogamento al caso puntiforme, vale: $$d\vec{E}=\frac{k\cdot dq}{r^2}\hat{r}$$
Se tale discorso lo estendiamo a tutto l'oggetto si ha: $$\bbox[#ffffff,5px,border:2px solid #ff6600]{|\vec{E}|=\int_Vd\vec{E}=k\int_V\frac{\cdot dq}{r^2}\hat{r}}$$
