Il moto uniformemente accelerato è un moto in cui l'accelerazione rimane costante: cioè un punto materiale varia la sua velocità sempre della stessa quantità $\Delta v$ in uguali intervalli di tempo $\Delta t$. Se l'accelerazione ha segno opposto rispetto alla velocità il moto si chiama moto unifomemente decelerato oppure uniformemente ritardato.
Di seguito schematizziamo le relazioni che sussistono tra velocità-tempo, spazio-tempo e spazio-velocità.
Assumeremo il verso della traiettoria sempre positivo, in modo che la velocità risulti positiva e quindi, nel caso di moto ritardato, l'accelerazione negativa.

Nella prima colonna, la relazione velocità-tempo rappresenta la legge secondo cui la velocità varia in funzione del tempo. La relazione è lineare e l'accelerazione rappresenta il coefficiente angolare della retta che ne esprime il grafico. Nel primo caso, l'accelerazione (e quindi il coefficiente angolare) è positiva, perciò la retta sarà crescente.
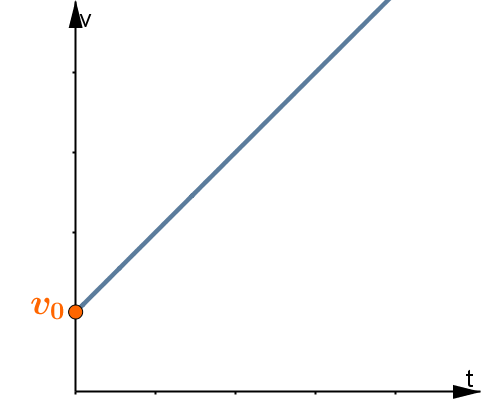
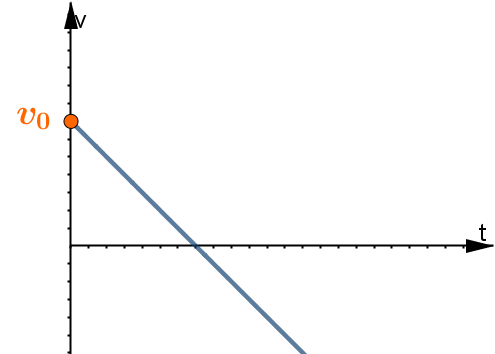
Nel secondo caso il coefficiente angolare negativo, determina una retta decrescente.
Nella seconda colonna è, poi rappresentato la relazione tra spazio e tempo: la relazione è quadratica quindi il suo grafico sarà un arco di parabola, con concavità verso l'alto o verso il basso a seconda del segno dell'accelerazione.
Infine, nell'ultima colonna, la relazione tra spazio e velocità che si è trovata, ricavando il tempo dalla prima colonna e andandolo a sostituire nella formula della seconda colonna.



