Analisi matematica
Questo é un corso dedicato a tutti quegli studenti che sono alle prese con esami quali Analisi Matematica I e II, Matematica Generale o Istituzioni di Matematica per economisti.
Il corso inizia con la presentazione degli insiemi numerici e le relazioni binarie che si possono creare tra di essi. Vengono definiti sup, inf, max, min, punti interni, di accumulazione e di frontiera per gli insiemi numerici e si studiano le successioni.
Si continua con il calcolo dei limiti e delle derivate, strumenti di analisi fondamentali per lo studio di funzioni e la loro rappresentazione nel piano cartesiano.
Strettamente legati al concetto di derivata sono gli integrali, indispensabili per il calcolo di aree sottese da funzioni nel piano. Studiamo dunque le equazioni differenziali, ossia delle equazioni in cui l’incognita é una funzione reale y la cui espressione viene determinata come somma di un integrale generale e una soluzione particolare.
Successivamente vediamo la convergenza di serie numeriche,
e serie di funzioni rivolgendo particolare attenzione alle serie di potenze e quindi agli sviluppi in serie di Taylor e Mc-Laurin.
Da questo punto in poi si va avanti trattando argomenti che sono comuni nei corsi avanzati di matematica, come per esempio corsi di Analisi II o Matematica Generale II. Si tratta di numeri complessi, e studio di funzioni di due variabili integrali doppi. curvilinei e superficiali e forme differenziali. Con l'aumento del numero di variabili, si può estendere anche il concetto di differenziabilità e integrazione multipla tramite il calcolo di integrali doppi, integrali tripli e forme differenziali. Infine, gli integrali curvilinei e superficiali completano il concetto di integrazione.
Calcolo delle derivate
Funzioni e loro rappresentazione nel piano cartesiano
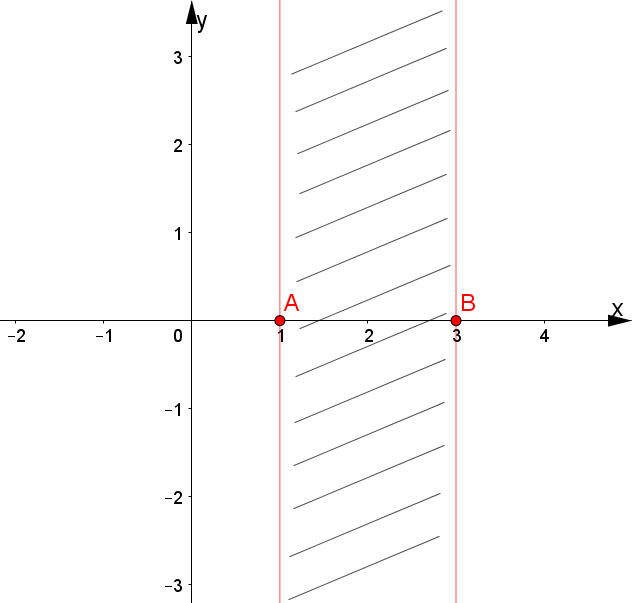
Dominio di funzioni
Positività o segno della funzione

Intersezione con gli assi cartesiani
Simmetrie: funzioni pari e dispari
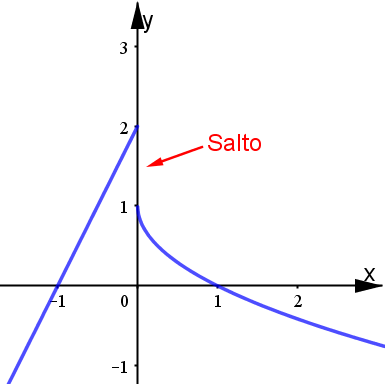
Punti di discontinuità
Limiti e asintoti
Monotonia e segno della derivata prima
Minimi e massimi relativi e assoluti
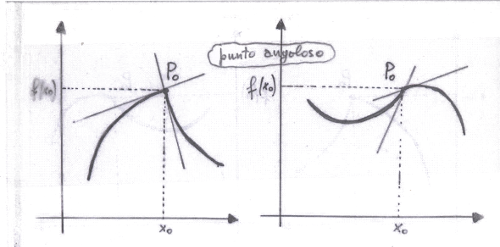
Punti di non derivabilità
Convessità e segno della derivata seconda
Punti di flesso

10.000 eserciziformazione completa
Eserciziari di Matematica Generale, Analisi I e II, Statistica, Fisica e Algebra Lineare