Massimo Comune Divisore tra monomi
La parte letterale del massimo comune divisore (M.C.D.) fra monomi è il prodotto delle solo lettere comuni a tutti i monomi, ognuna presa una sola volta e con l'esponente minimo. Il coefficiente scelto sarà il M.C.D. dei coefficienti dei monomi. Se i coefficienti dei monomi sono frazionari, per semplicità prenderemo M.C.D.=1.

Esempio
Esempio di calcolo dell'M.C.D. tra monomi.
- M.C.D.$\left(\frac{1}{2}x^3yz^4,\ \frac{3}{5}x^2y^3\right)=x^2y$
- M.C.D.$(10x^4y^3z,\ 12xy^2z^2)=\mbox{M.C.D.}(10,12)\cdot\mbox{M.C.D.}(x^4y^3z,\ xy^2z^2)=2xy^2z$
- M.C.D.$\left(\frac{3}{4}a^4bc^3,\ \frac{1}{2}a^3c^2d,\ -7a^2b^3c^5\right)=a^2c^2$
- M.C.D.$(12x^3y,\ -27xy^3,\ 42y^2)=\mbox{M.C.D.}(12,27,42)\cdot\mbox{M.C.D.}(x^3y,\ xy^3,\ y^2)=3y$
Osserviamo che l'M.C.D. tra 12, 27 e 42 è stato calcolato scomponendo in fattori primi i singoli numeri:
$$12=2^2\cdot 3,\quad 27=3^3,\quad 42=2\cdot 3\cdot 7$$
e prendendo i fattori comuni con l'esponente più basso (nell'esempio è il 3).
Minimo Comune Multiplo tra monomi
La parte letterale del minimo comune multiplo (m.c.m.) fra monomi è il prodotto di tutte le lettere presenti nei monomi, ognuna presa una sola volta con l'esponente massimo. Il coefficiente scelto sarà il m.c.m. dei coefficienti dei monomi. Se i coefficienti dei monomi sono frazionari, per semplicità prenderemo m.c.m.=1.
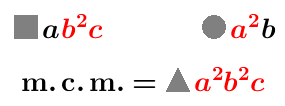
Esempio
Esempio di calcolo dell'm.c.m. tra monomi.
- m.c.m.$\left(\frac{1}{2}x^3yz^4,\ \frac{3}{5}x^2y^3\right)=x^3y^3z^4$
- m.c.m.$(10x^4y^3z,\ 12xy^2z^2)=\mbox{m.c.m.}(10,12)\cdot\mbox{m.c.m.}(x^4y^3z,\ xy^2z^2)=60x^4y^3z^2$
- m.c.m.$\left(\frac{3}{4}a^4bc^3,\ \frac{1}{2}a^3c^2d,\ -7a^2b^3c^5\right)=a^4b^3c^5$
- m.c.m.$(12x^3y,\ -27xy^3,\ 42y^2)=\mbox{m.c.m.}(12,27,42)\cdot\mbox{m.c.m.}(x^3y,\ xy^3,\ y^2)=756x^3y^3$
Osserviamo che l'm.c.m. tra 12, 27 e 42 è stato calcolato scomponendo in fattori primi i singoli numeri:
$$12=2^2\cdot 3,\quad 27=3^3,\quad 42=2\cdot 3\cdot 7$$
e prendendo i fattori comuni e non comuni con l'esponente più alto (nell'esempio è il $2^2\cdot 3^3\cdot 7=756$).



