Per risolvere un'equazione cercheremo di trasformarla in equazioni equivalenti, via via più semplici, fino a giungere a un'equazione in cui sia immediato trovare delle soluzioni.
Le regole di trasformazione di un'equazione in altre equazioni a essa equivalenti sono stabilite da 2 principi, chiamati principi di equivalenza
Primo principio di equivalenza
Data un'equazione, se si aggiunge ai due membri uno stesso numero (positivo o negativo) o una stessa espressione, si ottiene un'equazione equivalente.

Esempio
Risolvere l'equazione $$7x-2=6x+1$$
Per eliminare il termine $+6x$ dal secondo membro, aggiungiamo a entrambi i membri il termine $-6x$:

Otteniamo l'equazione $$x-2=1$$
Per eliminare $-2$ dal primo membro, aggiungiamo ai due membri $+2$:

Otteniamo così la soluzione dell'equazione $$x=3$$
Si può rendere più rapido il procedimento di risoluzione dell'equazione notando che, quando si elimina da un membro un termine, esso ricompare nell'altro con il segno cambiato. Possiamo dunque riformulare il primo principio di equivalenza come segue:
Regola del trasporto: data un'equazione, se ne ottiene una equivalente se si trasporta un termine da un membro all'altro, cambiandolo di segno.
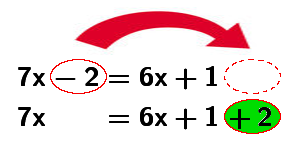
Con considerazione analoghe si giunge alla:
Regola di cancellazione: termini uguali presenti in entrambi i membri di un'equazione possono essere soppressi, ottenendo un'equazione equivalente.
Esempio
Risolvere l'equazione $$x+9=4+9$$ applicando il principio di cancellazione.
L'equazione data è equivalente a $$x=4$$. Infatti, quest'ultima si ottiene da quella data cancellando il $9$ sia a primo che a secondo membro della prima equazione.
Secondo principio di equivalenza
Data un'equazione, si ottiene un'equazione equivalente se si moltiplicano o si dividono i due membri per lo stesso numero, o espressione, diversi da zero.

Esempio
Risolvere l'equazione $$\frac{2}{3}x=10$$ applicando il secondo principio di equivalenza.
Moltiplichiamo per $3$ ambo i membri e otteniamo $$3\cdot\frac{2}{3}x=3\cdot 10,\quad\mbox{ossia}\quad 2x=30$$
Dividiamo i due membri per $2$ e otteniamo l'equazione $$\begin{eqnarray*}\frac{2x}{2}&=&\frac{30}{2},\\ x&=&15\end{eqnarray*}$$ che rappresenta la soluzione dell'equazione di partenza.
Consideriamo adesso l'equazione $$2=\frac{2}{x-1}$$
Dopo aver imposto la condizione di esistenza $x-1\neq 0$ ossia $x\neq 1$, moltiplichiamo ambo i membri per $x-1$. Otteniamo l'equazione: $$\begin{eqnarray*}2(x-1)&=&\frac{4}{x-1}(x-1)\\ 2x-2&=&4\end{eqnarray*}$$
Trasportiamo il $-2$ al secondo membro cambiandolo di segno $$\begin{eqnarray*}2x&=&4-2\\ 2x&=&2\end{eqnarray*}$$ e per finire dividiamo ambo i membri per $2$, ottenendo la soluzione $x=2$.
Osserviamo che applicando il secondo principio di equivalenza, è possibile ricavare altre due regole per risolvere le equazioni.
Regola della divisione per un fattore comune diverso da zero: quando tutti i termini di un'equazione hanno un fattore numerico comune (diverso da zero), si ottiene un'equazione equivalente dividendo tutti i termini per quel fattore.
Esempio
Nell'equazione $$3x+9=24-3$$ i termini $3x,9,24$ e $6$ sono tutti divisibili per $3$; pertanto possiamo dividere ciascun termine per $3$, ottenendo l'equazione $$x+3=8-1$$ equivalente alla data.
Regola del cambiamento di segno: cambiando segno a tutti i termini di un'equazione, si ottiene un'equazione equivalente.
Esempio
L'equazione $$-5x+8=-23$$ è equivalente all'equazione $$5x-8=23$$
Abbiamo cambiato il segno a tutti i termini dell'equazione: ciò equivale a moltiplicare i due membri dell'equazione per $-1$!.



