Di seguito trovi alcuni esercizi di logica sugli insiemi estratti dall'ultima banca dati presente online. Questi esercizi sono utili sia per superare la prova preselettiva nei concorsi pubblici che per accedere alla maggior parte dei corsi universitari a numero chiuso.
Ho scelto quelli più significativi ma invito a chiunque mi legge di contattarmi per richiedere la risoluzione di quesiti sulle relazioni insiemistiche di tipologia o difficoltà diversa da quelli qui presenti.
Individuare il diagramma che soddisfa la relazione insiemistica esistente tra i termini dati: Porti, Capitani, Barche a vela.
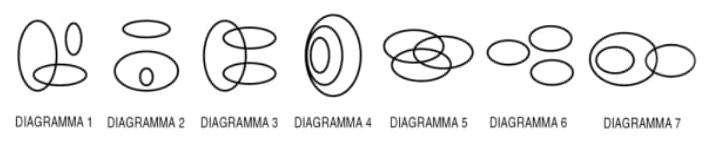
I tre termini, nonostante siano strettamente legati tra loro, appartengono a categorie diverse essendo. Infatti, i Porti sono dei luoghi, i Capitani delle persone e le Barche a vela dei mezzi di trasporto. In altre parole, questi 3 termini appartengono a degli insiemi disgiunti (che non si intersecano), per cui il diagramma che descrive la relazione insiemistica è il DIAGRAMMA 6.
Individuare il diagramma che soddisfa la relazione insiemistica esistente tra i termini dati: Numeri divisibili per 8, Numeri pari, Numeri divisibili per 80.
Indichiamo con
Innanzitutto notiamo che $$\begin{array}{l} 80=2^4\cdot 5\\ 8=2^3\end{array}$$
Tra tutti i numeri pari ci sono sicuramente quelli divisibili per 8, quindi B è contenuto in C ($B\subset C$). I numeri divisibili per 80 sono sicuramente pari (dato che nella fattorizzazione prima di 80 compare una potenza di 2) e divisibili per 8, quindi B e C sono contenuti in A ($B,C\subset A$). La relazione insiemistica scritta in simboli è $$B\subset C\subset A$$ e il diagramma che la descrive è quello a matriosca, ossia il DIAGRAMMA 4
Individuare il diagramma che soddisfa la relazione insiemistica esistente tra i termini dati: Tennisti, Campioni di tennis, Neonati.
Indichiamo con
I neonati non possono essere nè dei tennisti nè tanto meno dei campioni di tennis, quindi C non si interseca con nessuno degli altri due insiemi. Tutti i campioni di tennis sono ovviamente dei tennisti, di conseguenza B è contenuto in A ($B\subset A$). Il diagramma corretto è il DIAGRAMMA 2.
Individuare il diagramma che soddisfa la relazione insiemistica esistente tra i termini dati: Opere d'arte preziose, Dipinti, Impressionisti.
Indichiamo con
Gli impressionisti sono delle persone, per cui non appartengono nè alla categoria delle opere d'arte nè a quella dei dipinti. In altre parole C è disgiunto. I dipinti possono essere delle opere d'arte preziose ma non tutti i dipinti sono opere d'arte preziose. Questo vuol dire semplicemente che A e B si intersecano. La relazione insiemistica è rappresentata dal DIAGRAMMA 1.
Individuare il diagramma che soddisfa la relazione insiemistica esistente tra i termini dati: Giornalisti, Amanti della musica rock, Fumatori.
Indichiamo con
I tre insiemi si intersecano certamente l'uno con l'altro perchè un giornalista può essere anche un amante della musica e un fumatore. Ma ci possono anche essere, ad esempio, giornalisti fumatori che non amano la musica rock e, al contrario, giornalisti che amano la musica rock ma non sono fumatori. Questa situazione è descritta dal DIAGRAMMA 5.
Individuare il diagramma che soddisfa la relazione insiemistica esistente tra i termini dati: Biondi, Persone con capelli ricci, Castani.
Indichiamo con
Notiamo subito che A e C sono disgiunti dato che una persona bionda non può anche essere castana e viceversa. Inoltre, sia i biondi che i castani possono avere i capelli ricci, per sia A che C intersecano B. La relazione insiemistica è rappresentata nel DIAGRAMMA 3.
Individuare il diagramma che soddisfa la relazione insiemistica esistente tra i termini dati: Lettere della parola Vocabolario, Lettera della parola Colori, Lettere della parola Vespa.
Indichiamo con
Osserviamo che tutte le lettere di Colori sono anche lettere presenti in Vocabolario, dunque $B\subset A$. La parola VESPA, non ha nessuna lettera in comune con COLORI ma ne condivide qualcuna con VOCABOLARIO (queste sono: V e A). Per tale ragione, C non interseca B ma interseca A. Stiamo parlando del DIAGRAMMA 7.
Eserciziari di Matematica Generale, Analisi I e II, Statistica, Fisica e Algebra Lineare
