Eserciziari di Matematica Generale, Analisi I e II, Statistica, Fisica e Algebra Lineare...
$\large{\lim\limits_{n\rightarrow +\infty}n^2\left [ e-\left(1+\frac{1}{n}\right)^n\right ]}$
Esercizio 1
Si prova che $\forall \ n\geq 1$ vale
$$e-\left (1+\frac{1}{n}\right )^n\geq\frac{e}{2n+2}$$
Pertanto
$$n^2\left [e-\left (1+\frac{1}{n}\right )^n\right ]\geq n^2\frac{e}{2n+2}\stackrel{n\to +\infty}{\longrightarrow} +\infty$$
e
$$n\left [e-\left (1+\frac{1}{n}\right )^n\right ]\geq n\frac{e}{2n+2}\stackrel{n\to +\infty}{\longrightarrow} \frac{e}{2}$$
L'esercizio non è chiaro?
Altri esercizi di matematica
Studio di funzioni svolti
Studio grafico di funzione definita a tratti
studentiScuola superiore
livello difficoltà
Esercizi di geometria piana
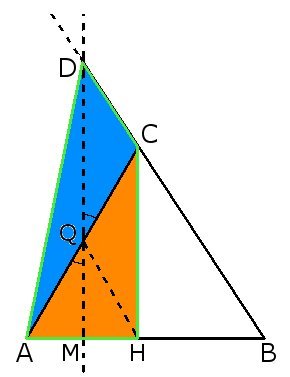
Equivalenza tra quadrilatero irregolare e triangolo isoscele
studentiScuola superiore
livello difficoltà

Esercizi sui limiti
Limiti di funzioni risolti mediante definizione
studentiScuola superiore
livello difficoltà

Esercizi sullo sviluppo in serie di Taylor e/o Mac Laurin
Sviluppo in serie di funzione logaritmica
studentiScuola superiore
livello difficoltà
Esercizi di geometria piana
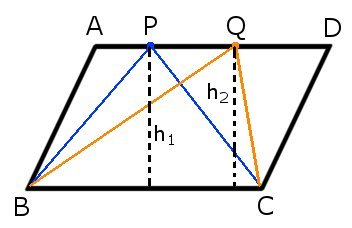
Equivalenza triangoli che si formano da un parallelogramma
studentiScuola superiore
livello difficoltà
studentiScuola superiore
livello difficoltà

Esercizi sullo sviluppo in serie di Taylor e/o Mac Laurin
Sviluppo in serie di Mc Laurin di un funzione con arcotangente
studentiScuola superiore
livello difficoltà

10.000 eserciziformazione completa
Eserciziari di Matematica Generale, Analisi I e II, Statistica, Fisica e Algebra Lineare