Se hai già visto come risolvere le equazioni esponenziali, sarai in grado di risolvere pure le disequazioni esponenziali avendo solo alcuni accorgimenti nel caso in cui la base dell'esponenziale è compresa tra 0 e 1.
Se invece vuoi provare tu stesso a risolvere le disequazioni esponenziali ne trovi tante in fondo alla pagina.
$$\frac{8^{1+x}+8^x}{9}\ge 4^{1+2x}+\frac{16}{4^{1-2x}}$$
Applicando le proprietà delle potenze quando necessario, seguiamo i seguenti passaggi:
$$\begin{array}{l}
\cfrac{8\cdot 8^{x}+8^x}{9}\ge 4\cdot 4^{2x}+\cfrac{16\cdot 4^{2x}}{4}\\ \cfrac{8^x(8+1)}{9}\ge 4\cdot 4^{2x}+4\cdot 4^{2x}\\ 8^x\ge8\cdot 4^{2x}\\ 2^{3x}\ge8\cdot 2^{4x}\\ \cfrac{2^{3x}}{2^{3x}}\ge\cfrac{8\cdot 2^{4x}}{2^{3x}}\\ 1\ge 8\cdot 2^{x}\\ 2^x\le \cfrac{1}{8}\\ 2^x\le\cfrac{1}{2^3}\\ 2^x\le 2^{-3}\\ x\le -3 \end{array}$$
$$\frac{4^{x-2}-5}{9^x-3} < 0$$
Questa è una disequazione esponenziale fratta. Per risolvere una disequazione fratta, poniamo numeratore e denominatore maggiori di 0:
Risolviamo la 1) prendendo i logaritmi in base 4 in entrambi i membri:
$$\begin{array}{l} 4^{x-2}>5\\ \log_4 4^{x-2}>\log_4 5\\ x-2>\log_4 5\\ x>\log_4 5+2\end{array}$$
Risolviamo la 2) notando che $9=3^2$:
$$\begin{array}{l} 9^x>3\\ 3^{2x}>3\\ 2x>1\\ x>\frac{1}{2}\end{array}$$
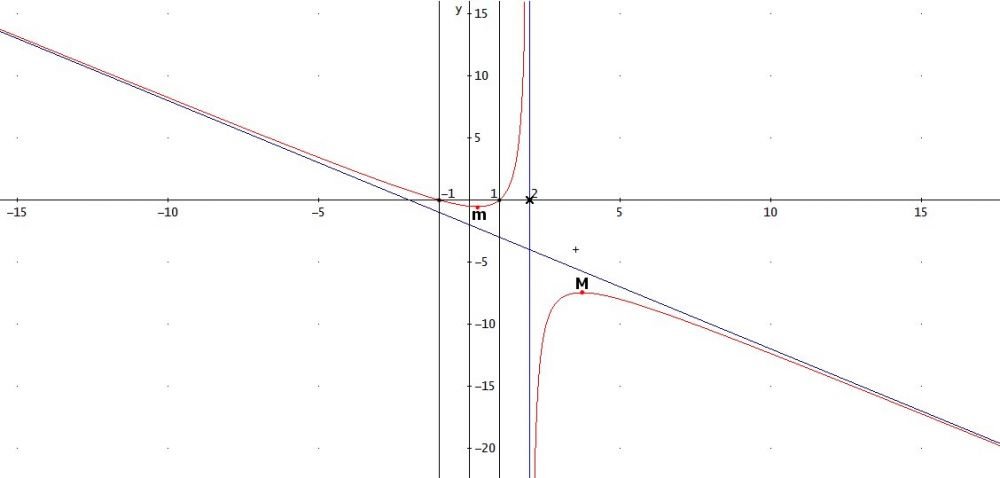
Dal prodotto dei segni delle due disequazioni otteniamo la soluzione $\frac{1}{2} < x < \log_4 5+2$ come conferma il grafico seguente:
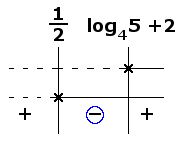
$$\left(\frac{9}{5}\right)^x < 0$$
L'esponenziale presente al primo membro, essendo per definizione una quantità positiva, non può mai essere minore di zero, per cui la disequazione esponenziale è impossibile.
$$\left(\frac{1}{3}\right)^{3x} > 27$$
Per le proprietà delle potenze, possiamo ribaltare la base dell'esponenziale al primo membro (da $1/3$ a $3$) e cambiare segno all'esponente; mentre il secondo membro lo possiamo riscrivere come potenza di 3 ($27=3^3$): $$3^{-3x}>3^3$$
Avendo due potenze con la stessa base in entrambi i membri, la precedente disequazione risulta equivalente alla disuguaglianza tra gli esponenti: $$-3x > 3$$ che è banalmente soddisfatta per $x < -1$.
$$2^{2x+1}+4^{x-1}+4^x < 13$$
Applichiamo anche in questo caso le proprietà delle potenze per riscrivere tutti gli esponenziali con una base comune ($2$): $$\begin{array}{l} 2^{2x}\cdot 2+2^{2x-2}+2^{2x}-13 < 0\\ 2\cdot 2^{2x}+2^{-2}\cdot 2^{2x}+2^{2x}-13 < 0\\ 2\cdot 2^{2x}+\frac{1}{4}\cdot 2^{2x}+2^{2x}-13 < 0\end{array}$$
Facciamo la seguente sostituzione: poniamo $t=2^{2x}$ e la disequazione esponenziale diventa una disequazione di primo grado $$\begin{array}{l} 2t+\frac{1}{4}t+t-13 < 0\\ \frac{8t+t+4t-52}{4} < 0\\ 13t-52 < 0\\ t < 4\end{array}$$
Infine, ripristinando il valore di $t=2^{2x}$ l'ultima disequazione diventa $$2^{2x} < 4$$ ossia $2^{2x} < 2^2$ che è soddisfatta per $2x < 2$ e quindi $x<1$.
$$2^{x^2-3x}>1$$
Trasformando $1$ in $2^0$, affiché la disuguaglianza sia verificata deve essere:
$$2^{x^2-3x}>2^0\\ x^2-3x>0 \\ x < 0\ \vee\ x>3$$
$$\left(\frac{1}{3}\right)^{2x-5}>\frac{1}{3}$$
Essendo le basi delle potenze minori di $1$, affinché la disuguaglianza sia verificata deve essere:
$$2x-5 < 1\\ x < 3$$
$$2^{\frac{x^2-11}{x+2}} < 4$$
Riscrivendo $4$ come $2^2$ la disequazione data è soddisfatta se e soltanto se è soddisfatta la seguente disequazione:
$$\frac{x^2-11}{x+2} < 2$$
In sostanza, la disuguaglianza tra due funzioni esponenziali è soddisfatta se e solo se è soddisfatta la disuguaglianza tra i rispettivi esponenti. Risolviamo, quindi, la disequazione appena ottenuta.
$$\begin{array}{l} \cfrac{x^2-11}{x+2}-2 < 0\\ \cfrac{x^2-11-2x-4}{x+2} < 0\\ \cfrac{x^2-2x-15}{x+2} < 0\end{array}$$
Quest'ultima disequazione di tipo fratta:
$$\begin{array}{l} \cfrac{x^2-2x-15}{x+2} < 0\\ N:x^2-2x-15 > 0\quad\Rightarrow\quad x < -3\ \vee x > 5\\ D:x+2 > 0\quad\Rightarrow\quad x>-2\end{array}$$
Facciamo il prodotto dei segni tra le due soluzioni ottenute:
Considerando solo le regioni negative del grafico, avremo che le soluzioni della disequazione iniziale sono:
$$x < -3\ \vee\ -2 < x < 5$$
Oppure analogamente possiamo scrivere:
$$]-\infty,-3[\ \cup\ ]-2,5[$$
Eserciziari di Matematica Generale, Analisi I e II, Statistica, Fisica e Algebra Lineare
